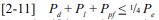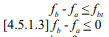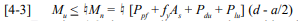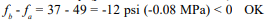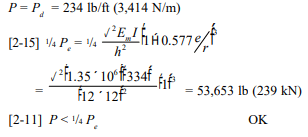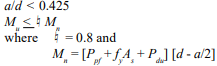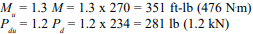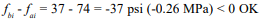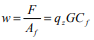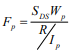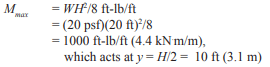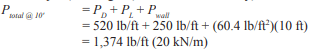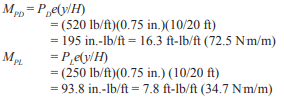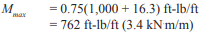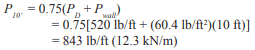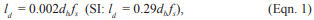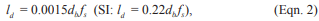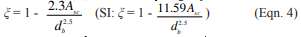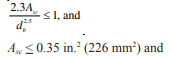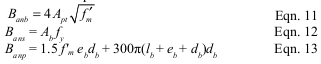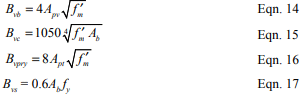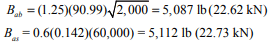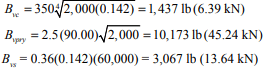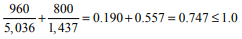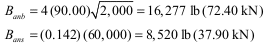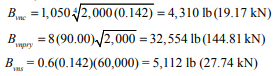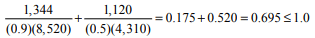Home / Technical Resources / allowable stress design

Resources

Post-Tensioned Concrete Masonry Wall Design

  • August 2018

INTRODUCTION

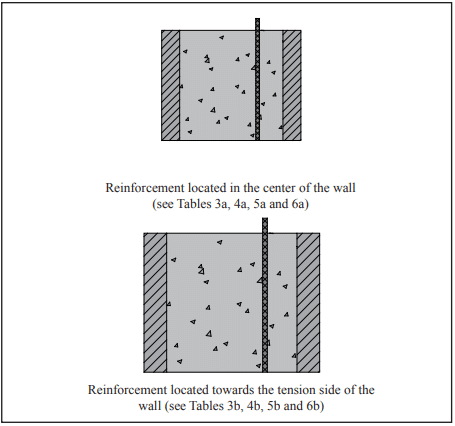
The 1999 Building Code Requirements for Masonry Structures, ACI 530/ASCE 5/TMS 402 (ref. 1), was the first masonry code in the United States to include general design provisions for prestressed masonry. Prestressing masonry is a process whereby internal compressive stresses are introduced to counteract tensile stresses resulting from applied loads. Compressive stresses are developed within the masonry by tensioning a steel tendon, which is anchored to the top and bottom of the masonry element (see Figure 1). Post-tensioning is the primary method of prestressing, where the tendons are stressed after the masonry has been placed. This TEK focuses on the design of concrete masonry walls constructed with vertical post-tensioned tendons.

Advantages

Prestressing has the potential to increase the flexural strength, shear strength and stiffness of a masonry element. In addition to increasing the strength of an element, prestressing forces can also close or minimize the formation of some cracks. Further, while research (refs. 14, 15) indicates that ductility and energy dissipation capacity are enhanced with prestressing, Building Code Requirements for Masonry Structures (ref. 1) conservatively does not take such performance into account.

Post-tensioned masonry can be an economical alternative to conventionally reinforced masonry. One major advantage of prestressing is that it allows a wall to be reinforced without the need for grout. Also, the number of prestressing tendons may be less than the number of reinforcing bars required for the same flexural strength.

Post-tensioning masonry is primarily applicable to walls, although it can also be used for beams, piers, and columns. Vertical post-tensioning is most effective for increasing the structural capacity of elements subjected to relatively low axial loads. Structural applications include loadbearing, nonloadbearing and shear walls of tall warehouses and gymnasiums, and commercial buildings, as well as retaining walls and sound barrier walls. Post-tensioning is also an option for strengthening existing walls.

Figure 1—Schematic of Typical Post-Tensioned Wall

MATERIALS

Post-tensioned wall construction uses standard materials: units, mortar, grout, and perhaps steel reinforcement. In addition, post-tensioning requires tendons, which are steel wires, bars or strands with a higher tensile strength than conventional reinforcement. Manufacturers of prestressing tendons must supply stress relaxation characteristics for their material if it is to be used as a prestressing tendon. Specifications for those materials used specifically for post-tensioning are given in Table 1. Other material specifications are covered in references 9 through 12. Construction is covered in  Post-Tensioned Concrete Masonry Wall Construction, TEK 03-14 (ref. 3).

Table 1—Post-Tensioned Material Specifications

CORROSION PROTECTION

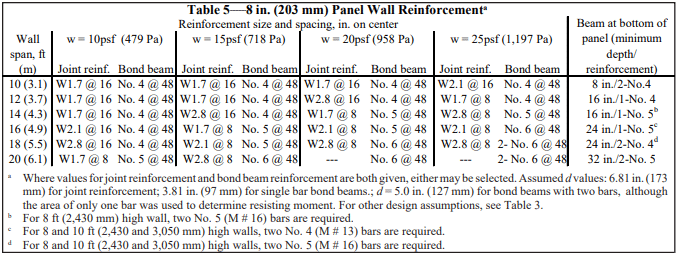
As with conventionally reinforced masonry structures, Building Code Requirements for Masonry Structures (ref. 1) mandates that prestressing tendons for post-tensioned masonry structures be protected against corrosion. As a minimum, the prestressing tendons, anchors, couplers and end fittings in exterior walls exposed to earth or weather must be protected. All other walls exposed to a mean relative humidity exceeding 75% must also employ some method of corrosion abatement. Unbonded tendons can be protected with galvanizing, epoxy coating, sheathing or other alternative method that provides an equivalent level of protection. Bonded tendons are protected from corrosion by the corrugated duct and prestressing grout in which they are encased.

DESIGN LOADS

As for other masonry structures, minimum required design loads are included in Minimum Design Loads for Buildings and Other Structures, ASCE 7 (ref. 5), or the governing building codes. If prestressing forces are intended to resist lateral loads from earthquake, a factor of 0.9 should be applied to the strength level prestress forces (0.6 for allowable stress design) as is done with gravity loads.

STRUCTURAL DESIGN

The design of post-tensioned masonry is based on allowable stress design procedures, except for laterally restrained tendons which use a strength design philosophy. Building Code Requirements for Masonry Structures (ref. 1) prescribes allowable stresses for unreinforced masonry in compression, tension and shear, which must be checked against the stresses resulting from applied loads.

The flexural strength of post-tensioned walls is governed by either the flexural tensile stress of the masonry (the flexural stress minus the post-tensioning and dead load stress), the masonry compressive stress, the tensile stress within the tendon, the shear capacity of the masonry or the buckling capacity of the wall.

Masonry stresses must be checked at the time of peak loading (independently accounting for both short-term and long-term losses), at the transfer of post-tensioning forces, and during the jacking operation when bearing stresses may be exceeded. Immediately after transfer of the post-tensioning forces, the stresses in the steel are the largest because long-term losses have not occurred. Further, because the masonry has had little time to cure, the stresses in the masonry will be closer to their capacity. Once long-term losses have transpired, the stresses in both the masonry and the steel are reduced. The result is a coincidental reduction in the effective capacity due to the prestressing force and an increase in the stresses the fully cured masonry can resist from external loads.

Effective Prestress

Over time, the level of prestressing force decreases due to creep and shrinkage of the masonry, relaxation of the prestressing tendons and potential decreases in the ambient temperature. These prestressing losses are in addition to seating and elastic shortening losses witnessed during the prestressing operation. In addition, the prestressing force of bonded tendons will decrease along the length of the tendon due to frictional losses. Since the effective prestressing force varies over time, the controlling stresses should be checked at several stages and loading conditions over the life of the structure.

The total prestress loss in concrete masonry can be assumed to be approximately 35%. At the time of transfer of the prestressing force, typical losses include: 1% seating loss + 1% elastic shortening = 2%. Additional losses at service loads and moment strength include:

relaxation3%
temperature10%
creep8%
CMU shrinkage7%
contingency5%
total33%

Prestress losses need to be estimated accurately for a safe and economical structural design. Underestimating losses will result in having less available strength than assumed. Overestimating losses may result in overstressing the wall in compression.

Effective Width

In theory, a post-tensioning force functions similarly to a concentrated load applied to the top of a wall. Concentrated loads are distributed over an effective width as discussed in the commentary on Building Code Requirements for Masonry Structures (ref. 1). A general rule-of-thumb is to use six times the wall thickness as the effective width.

Elastic shortening during post-tensioning can reduce the stress in adjacent tendons that have already been stressed. Spacing the tendons further apart than the effective width theoretically does not reduce the compressive stress in the effective width due to the post-tensioning of subsequent tendons. The applied loads must also be consolidated into the effective width so the masonry stresses can be determined. These stresses must be checked in the design stage to avoid overstressing the masonry.

Flexure

Tensile and compressive stresses resulting from bending moments applied to a section are determined in accordance with conventional elastic beam theory. This results in a triangular stress distribution for the masonry in both tension and compression. Maximum bending stress at the extreme fibers are determined by dividing the applied moment by the section modulus based on the minimum net section.

Net Flexural Tensile Stress

Sufficient post-tensioning force needs to be provided so the net flexural tensile stress is less than the allowable values. Flexural cracking should not occur if post-tensioning forces are kept within acceptable bounds. Flexural cracking due to sustained post-tensioning forces is believed to be more severe than cracking due to transient loading. Flexural cracks due to eccentric post-tensioning forces will remain open throughout the life of the wall, and may create problems related to water penetration, freeze-thaw or corrosion. For this reason, Building Code Requirements for Masonry Structures (ref. 1) requires that the net flexural tensile stress be limited to zero at transfer of the post-tensioning force and for service loadings with gravity loads only.

Axial Compression

Compressive stresses are determined by dividing the sum of the post-tensioning and gravity forces by the net area of the section. They must be less than the code prescribed (ref. 1) allowable values of axial compressive stress.

Walls must also be checked for buckling due to gravity loads and post-tensioning forces from unrestrained tendons. Laterally restrained tendons can not cause buckling; therefore only gravity compressive forces need to be checked for buckling in walls using laterally restrained tendons. Restraining the tendons also ensures that the tendons do not move laterally in the wall when the masonry deflects. The maximum compressive force that can be applied to the wall based upon ¼ buckling is Pe, per equation 2-11 of Building Code Requirements for Masonry Structures (ref. 1).

Combined Axial and Flexural Compressive Stress

Axial compressive stresses due to post-tensioning and gravity forces combine with flexural compressive stresses at the extreme fiber to result in maximum compressive stress. Conversely, the axial compressive stresses combine with the flexural tensile stresses to reduce the absolute extreme fiber stresses. To ensure the combination of these stresses does not exceed code prescribed allowable stresses, a unity equation is checked to verify compliance. Employing this unity equation, the sum of the ratios of applied-to-allowable axial and flexural stresses must be less than one. Unless standards (ref. 5) limit its use, an additional one-third increase in allowable stresses is permitted for wind and earthquake loadings, as is customary with unreinforced and reinforced masonry. Further, for the stress condition immediately after transfer of the post-tensioning force, a 20% increase in allowable axial and bending stresses is permitted by Building Code Requirements for Masonry Structures (ref. 1).

Shear

As with all stresses, shear stresses are resisted by the net area of masonry, and the wall is sized such that the maximum shear stress is less than the allowable stress. In addition, the compressive stress due to post-tensioning can be relied on to increase allowable shear stresses in some circumstances.

Post-Tensioning Tendons

The stress in the tendons is limited (ref. 1) such that:

  1. the stress due to the jacking force does not exceed 0.94fpy, 0.80fpu, nor that recommended by the manufacturer of the tendons or anchorages,
  2. the stress immediately after transfer does not exceed 0.82fpy nor 0.74fpu, and
  3. the stress in the tendons at anchorages and couplers does not exceed 0.78fpy nor 0.70fpu.

DETERMINATION OF POST-TENSIONING FORCES

Case (a) after prestress losses and at peak loading:

Assuming that the moment, M, due to wind or earthquake loadings is large relative to the eccentric load moment, the critical location will be at the mid-height of the wall for simply-supported walls, and the following equations apply (bracketed numbers are the applicable Building Code Requirements for Masonry Structures (ref. 1) equation or section numbers):

The 1.33 factor in Equation [2-10] represents the one- third increase in allowable stress permitted for wind and earthquake loadings. If the moment, M, is a result of soil pressures (as is the case for retaining walls), the 1.33 factor in Equation [2-10] must be replaced by 1.00.

Note that if the tendons are laterally restrained, Ppf should not be included in Equation [2-11].

(under the load combination of prestressing force and dead load only)

Additional strength design requirements for laterally restrained tendons:

Equation 4-3 above applies to members with uniform width, concentric reinforcement and prestressing tendons and concentric axial load. The nominal moment strength for other conditions should be determined based on static moment equilibrium equations.

Case (b) at transfer of post-tensioning:

Assuming that vertical live loads are not present during post-tensioning, the following equations apply. The worst case is at the top of the wall where post-tensioning forces are applied.

For cantilevered walls, these equations must be modified to the base of the wall.

If the eccentricity of the live load, Pl, is small, neglecting the live load in Equation [2-10] may also govern.

Case (c) bearing stresses at jacking:

Bearing stresses at the prestressing anchorage should be checked at the time of jacking. The maximum allowable bearing stress at jacking is 0.50f’mi per Building Code Requirements for Masonry Structures (ref. 1) section 4.9.4.2.

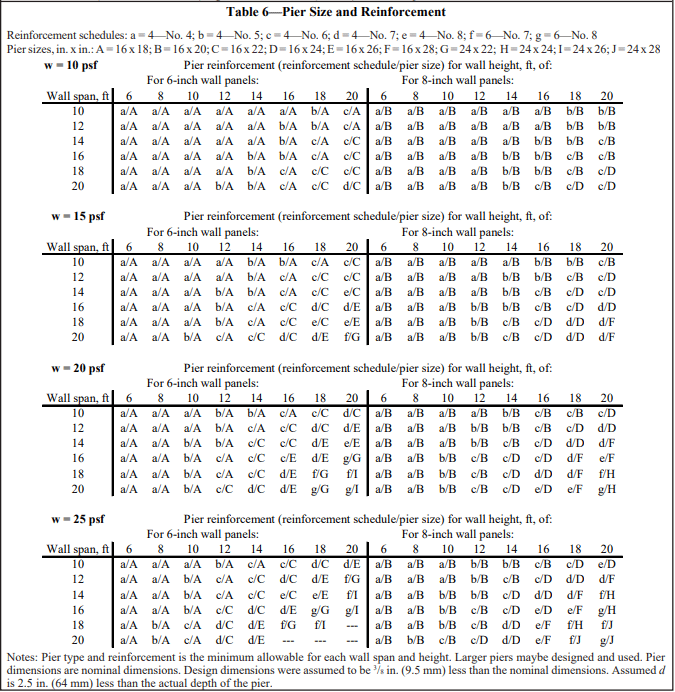
DESIGN EXAMPLE

Design a simply-supported exterior wall 12 ft (3.7 m) high for a wind load of 15 psf (0.72 kPa). The wall is constructed of concrete masonry units complying with ASTM C 90 (ref. 6). The units are laid in a full bed of Type S Portland cement lime mortar complying with ASTM C 270 (ref. 7). The specified compressive strength of the masonry (f’m) is 1,500 psi (10.3 MPa). The wall will be post-tensioned with 7/16 in. (11 mm) diameter laterally restrained tendons when the wall achieves a compressive strength of 1,250 psi (8.6 MPa). Axial load and prestress are concentric.

Given:
8 in. (203 mm) CMU
tf = 1.25 in. (32 mm)
f’m = 1,500 psi (10.3 MPa)
f’mi = 1,250 psi (8.6 MPa)
Fbt = 25 psi (0.17 MPa) (Type S Portland cement/lime mortar)
fpy = 100 ksi (690 MPa) (bars)
fpu = 122 ksi (840 MPa)
Aps = 0.14 in² (92 mm²)
Es = 29 x 106 psi (200 GPa)
Em = 900 f’m = 1.35 x 106 psi (9,300 MPa)
n = Es/Em = 21.5
d = 7.625/2 in. = 3.81 in. (97 mm) (tendons placed in the center of the wall)
unit weight of CMU wall = 39 psf (190 kg/m²) (ref. 13)

Loads: M = wh²/8 = (15)(12)²/8 = 270 ft-lb (366 N-m)
Pd at mid-height = (39)(12)/2 = 234 lb/foot of wall (3,410 N/m) (Pl = 0)

Maximum tendon stresses:
Determine governing stresses based on code limits (ref. 1):

At jacking:0.94 fpy = 94.0 ksi (648 MPa)
0.80 fpu = 97.6 ksi (673 MPa)
At transfer:0.82 fpy = 82.0 ksi (565 MPa)
0.74 fpu = 90.3 ksi (623 MPa)
At service loads:0.78 fpy = 78.0 ksi (538 MPa) ⇒ governs
0.70 fpu = 85.4 ksi (589 MPa)

Because the tendon’s specified tensile strength is less than 150 ksi (1,034 MPa), fps = fse (per ref. 1 section 4.5.3.3.4).

Prestress losses: Assume 35% total loss (as described in the Effective Prestress section above).

Tendon forces:
Determine the maximum tendon force, based on the governing tendon stress determined above for each case of jacking, transfer and service. At transfer, include 2% prestress losses. At service, include the full 35% losses.
Tendon capacity at jacking = 0.94 fpyAps = 13.3 kips (59 kN)
Tendon capacity at transfer = 0.82 fpyAps A x 0.98 = 11.4 kips (51 kN) (including transfer losses)
Tendon capacity at service = 0.78 fpyAps A x 0.65 = 7.2 kips (32 kN) (including total losses)

Try tendons at 48 in. (1,219 mm) on center (note that this tendon spacing also corresponds to the maximum effective prestressing width of six times the wall thickness).

Determine prestressing force, based on tendon capacity determined above:
at transfer: Ppi = 11.4 kips/4 ft = 2,850 lb/ft (41.6 kN/m)
at service: Ppf = 7.2 kips/4 ft = 1,800 lb/ft (26.3 kN/m)

Wall section properties: (ref. 8)
8 in. (203 mm) CMU with full mortar bedding:
An = 41.5 in.²/ft (87,900 mm²/m)
I = 334 in.4/ft (456 x 106 mm4/m)
S = 87.6 in.³/ft (4.71 x 106 mm³/m)
r = 2.84 in. (72.1 mm)

At service loads:
At service, the following are checked: combined axial compression and flexure using the unity equation (equation 2-10); net tension in the wall; stability by ensuring the compressive load does not exceed one-fourth of the buckling load, Pe, and shear and moment strength.

Check combined axial compression and flexure:

Check tension for load combination of prestress force and dead load only (per ref. 1 section 4.5.1.3):

Check stability:
Because the tendons are laterally restrained, the prestressing force, Ppf, is not considered in the determination of axial load ( per ref. 1 section 4.5.3.2), and the wall is not subject to live load in this case, so equation 2-11 reduces to:

Check moment strength:
Building Code Requirements for Masonry Structures section 4.5.3.3 includes the following criteria for moment strength of walls with laterally restrained tendons:

In addition, the compression zone must fall within the masonry, so a < tf.

where 1.3 and 1.2 are load factors for wind and dead loads, respectively.

At transfer:
Check combined axial compression and flexure using the unity equation (equation 2-10) and net tension in the wall.

Check tension for load combination of prestress force and dead load only (per ref. 1 section 4.5.1.3):

Therefore, use 7/16 in. (11 mm) diameter tendons at 48 in. (1,219 mm) o.c. Note that although wall design is seldom governed by out-of-plane shear, the shear capacity should also be checked.

NOTATIONS

An     net cross-sectional area of masonry section, in.² (mm²)
Aps   threaded area of post-tensioning tendon, in.² (mm²)
As     cross-sectional area of mild reinforcement, in.² (mm²)
a       depth of an equivalent compression zone at nominal strength, in. (mm)
b        width of section, in. (mm)
d       distance from extreme compression fiber to centroid of prestressing tendon, in. (mm)
Es      modulus of elasticity of prestressing steel, psi (MPa)
Em    modulus of elasticity of masonry, psi (MPa)
ed      eccentricity of dead load, in. (mm)
el       eccentricity of live load, in. (mm)
ep      eccentricity of post-tensioning load, in. (mm)
Fa     allowable masonry axial compressive stress, psi (MPa)
Fai    allowable masonry axial compressive stress at transfer, psi (MPa)
Fb     allowable masonry flexural compressive stress, psi (MPa)
Fbi    allowable masonry flexural compressive stress at transfer, psi (MPa)
Fbt    allowable flexural tensile strength of masonry, psi (MPa)
fa      axial stress after prestress loss, psi (MPa)
fai     axial stress at transfer, psi (MPa)
fb      flexural stress after prestress loss, psi (MPa)
fbi     flexural stress at transfer, psi (MPa)
f’m    specified compressive strength of masonry, psi (MPa)
f’mi   specified compressive strength of masonry at time of transfer of prestress, psi (MPa)
fps    stress in prestressing tendon at nominal strength, psi (MPa)
fpu    specified tensile strength of prestressing tendon, ksi (MPa)
fpy    specified yield strength of prestressing tendon, ksi (MPa)
fse     effective stress in prestressing tendon after all pre-stress losses have occurred, psi (MPa)
fy     specified yield strength of steel for reinforcement and anchors, psi (MPa)
h      masonry wall height, in. (mm)
I       moment of inertia of net wall section of extreme fiber tension or compression, in.4/ft (mm4/m)
M    moment due to lateral loads, ft-lb (N⋅m)
Mn   nominal moment strength, ft-lb (N⋅m)
Mu   factored moment due to lateral loads, ft-lb (N⋅m)
n      modular ratio of prestressing steel and masonry (Es/Em)
Pd    axial dead load, lb/ft (kN/m)
Pdu  factored axial dead load, lb/ft (kN/m)
Pe    Euler buckling load, lb/ft (kN/m)
Pl     axial live load, lb/ft (kN/m)
Plu    factored axial live load, lb/ft (kN/m)
Ppi    prestress force at transfer, lb/ft (kN/m)
Ppf    prestress force including losses, lb/ft (kN/m)
r       radius of gyration for net wall section, in. (mm)
S       section modulus of net cross-sectional area of the wall, in.³ /ft (mm³/m)
tf       face shell thickness of concrete masonry, in. (mm)
w     applied wind pressure, psf (kPa)
¤      strength reduction factor = 0.8

REFERENCES

  1. Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
  2. Building Code Requirements for Structural Concrete, ACI 318-99. Detroit, MI: American Concrete Institute, Revised 1999.
  3. Construction of Post-Tensioned Concrete Masonry Walls, TEK 03-14. Concrete Masonry & Hardscapes Association, 2002.
  4. International Building Code. International Code Council, 2000.
  5. Minimum Design Loads for Buildings and Other Structures, ASCE 7-98, American Society of Civil Engineers, 1998.
  6. Standard Specification for Loadbearing Concrete Masonry Units, ASTM C 90-01a. American Society for Testing and Materials, 2001.
  7. Standard Specification for Mortar for Unit Masonry, ASTM C 270-01. American Society for Testing and Materials, 2001.
  8. Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.
  9. Concrete Masonry Unit Shapes, Sizes, Properties, and Specifications, CMU-TEC-001-23, Concrete Masonry & Hardscapes Association, 2023.
  10. Mortars for Concrete Masonry, TEK 09-01A. Concrete Masonry & Hardscapes Association, 2001.
  11. Grout for Concrete Masonry, TEK 09-04. Concrete Masonry & Hardscapes Association, 2005.
  12. Steel for Concrete Masonry Reinforcement, TEK 12-04D. Concrete Masonry & Hardscapes Association, 1998.
  13. Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.
  14. Schultz, A.E., and M.J. Scolforo, An Overview of Prestressed Masonry, TMS Journal, Vol. 10, No. 1, August 1991, pp. 6-21.
  15. Schultz, A.E., and M.J. Scolforo, Engineering Design Provisions for Prestressed Masonry, Part 1: Masonry Stresses, Part 2: Steel Stresses and Other Considerations, TMS Journal, Vol. 10, No. 2, February 1992, pp. 29-64.
  16. Standard Specification for Steel Strand, Uncoated Seven-Wire for Prestressed Concrete, ASTM A 416-99. American Society for Testing and Materials, 1999.
  17. Standard Specification for Uncoated Stress-Relieved Steel Wire for Prestressed Concrete, ASTM A 421-98a. American Society for Testing and Materials, 1998.
  18. Standard Specification for Uncoated High-Strength Steel Bar for Prestressed Concrete, ASTM A 722-98. American Society for Testing and Materials, 1998.
  19. Standard Specification for Compressible-Washer-Type Direct Tension Indicators for Use with Structural Fasteners, ASTM F 959-01a. American Society for Testing and Materials, 2001.

ASD Tables for Reinforced Concrete Masonry Walls Based on the 2012 IBC & 2011 MSJC

  • August 2018

INTRODUCTION

The combination of concrete masonry and steel reinforcement provides a strong structural system capable of resisting large compressive and flexural loads. Reinforced masonry structures have significantly higher flexural strength and ductility than similarly configured unreinforced structures and provide greater reliability in terms of expected load carrying capacity at failure.

Concrete masonry elements can be designed using several methods in accordance with the International Building Code (IBC, ref. 1) and, by reference, Building Code Requirements for Masonry Structures (MSJC Code, ref. 2): allowable stress design, strength design, direct design, empirical design, or prestressed masonry. The design tables in this TEK are based on allowable stress design provisions.

The content presented in this edition of TEK 14-19B is based on the requirements of the 2012 IBC (ref. 1a), which in turn references the 2011 edition of the MSJC Code (ref. 2a). For designs based on the 2006 or 2009 IBC (refs. 1b, 1c), which reference the 2005 and 2008 MSJC (refs. 2b, 3c), respectively, the reader is referred to TEK 14-19B (ref. 3).

Significant changes were made to the allowable stress design (ASD) method between the 2009 and 2012 editions of the IBC. These are described in detail in TEK 14-07C, ASD of Concrete Masonry (2012 IBC & 2011 MSJC) (ref. 4), along with a detailed presentation of all of the allowable stress design provisions of the 2012 IBC.

LOAD TABLES

Tables 1 and 2 list the maximum bending moments and shears, respectively, imposed on walls simply supported at the top and bottom and subjected to uniform lateral loads with no applied axial loads.

Table 1—Required Moment Strength for Walls Subjected to Uniform Lateral Loads
Table 2—Required Shear Strength for Walls Subjected to Uniform Lateral Loads

A Based on walls simply supported at top and bottom, no axial load.

WALL CAPACITY TABLES

Tables 3, 4, 5 and 6 contain the maximum bending moments and shear loads that can be sustained by 8-, 10-, 12-, and 16-in. (203-, 254-, 305-, 406 mm) walls, respectively, without exceeding the allowable stresses defined in the 2012 IBC and 2011 MSJC (refs. 1a, 2a). These wall strengths can be compared to the loads in Tables 1 and 2 to ensure the wall under consideration has sufficient design capacity to resist the applied load.

The values in Tables 3 through 6 are based on the following criteria:

  • Maximum allowable stresses:
  • f’m = 1500 psi (10.3 MPa)
  • Em  = 900f’m or 1,350,000 psi (9,310 MPa)
  • Es = 29,000,000 psi (200,000 MPa)
  • Type M or S mortar
  • running bond or bond beams at 48 in. (1,219 mm) max o.c.
  • reinforcement spacing does not exceed the wall height
  • only cores containing reinforcement are grouted.

Reinforcing Steel Location

Two sets of tables are presented for each wall thickness. Tables 3a, 4a, 5a and 6a list resisting moment and resisting shear values for walls with the reinforcing steel located in the center of the wall. Centered reinforcing bars are effective for providing tensile resistance for walls which may be loaded from either side, such as an above grade exterior wall which is likely to experience both wind pressure and suction.

Tables 3b, 4b, 5b and 6b list resisting moment and resisting shear values for walls with the reinforcing steel offset from the center.

Placing the reinforcement farther from the compression face of the masonry provides a larger effective depth of reinforcement, d, and correspondingly larger capacities. A single layer of off-center reinforcement can be used in situations where the wall is loaded from one side only, such as a basement wall with the reinforcement located towards the interior. For walls where loads can be in both directions (i.e. pressure or suction), two layers of reinforcement are used: one towards the wall exterior and one towards the interior to provide increased capacity under both loading conditions. In Tables 3b, 4b, 5b and 6b, the effective depth of reinforcement, d, is a practical value which takes into account construction tolerances and the reinforcing bar diameter.

Figure 1 illustrates the two steel location cases.

Figure 1—Reinforcing Steel Locations
Table 3—Allowable Stress Design Capacities for 8-in. (203-mm) WallsA

  
  

  
  

  
  

Figure 1—Reinforcing Steel Locations
Table 4—Allowable Stress Design Capacities for 10-in. (254-mm) WallsA
Table 5—Allowable Stress Design Capacities for 12-in. (305-mm) WallsA
Table 6—Allowable Stress Design Capacities for 16-in. (406-mm) WallsA

DESIGN EXAMPLE

A warehouse wall will span 34 ft (10.4 m) between the floor slab and roof diaphragm. The walls will be constructed using 12 in. (305 mm) concrete masonry units. What is the required reinforcing steel size and spacing to support a wind load of 20 psf (0.96 kPa)?

From interpolation of Tables 1 and 2, respectively, the wall must be able to resist:
M = 34,800 lb-in./ft (12.9 kN-m/m)
V = 340 lb/ft (4.96 kN/m)

Assuming the use of offset reinforcement, from Table 5b, No. 6 bars at 40 in. on center (M#19 at 1,016 mm) or No. 7 bars at 48 in. (M#22 at 1,219 mm) on center provides sufficient strength: for No. 6 bars at 40 in. o.c. (M#19 at 1,016 mm):
Mr = 35,686 lb-in./ft (13.3 kN-m/m) > M             OK
Vr = 2,299 lb/ft (33.5 kN/m) > V                           OK

for No. 7 bars at 48 in. (M#22 at 1,219 mm) :
Mr = 40,192 lb-in./ft (14.9 kN-m/m) > M              OK
Vr = 2,133 lb/ft (31.1 kN/m) > V                            OK

As discussed above, since wind loads can act in either direction, two bars must be provided in each cell when using off-center reinforcement—one close to each faceshell.

Alternatively, No. 6 bars at 24 in (M#19 at 610 mm) or No. 8 at 40 in (M#25 at 1,016 mm) could have been used in the center of the wall.

NOTATION

As   = area of nonprestressed longitudinal reinforcement, in.² (mm²)
b     = effective compressive width per bar, in. (mm)
d     = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
Em  = modulus of elasticity of masonry in compression, psi (MPa)
Es   = modulus of elasticity of steel, psi (MPa)
Fb   = allowable compressive stress available to resist flexure only, psi (MPa)
Fs    = allowable tensile or compressive stress in reinforcement, psi (MPa)
Fv    = allowable shear stress, psi (MPa)
f’m   = specified compressive strength of masonry, psi (MPa)
M    = maximum calculated bending moment at section under consideration, in.-lb, (N-mm)
Mr   = flexural strength (resisting moment), in.-lb (N-mm)
V     = shear force, lb (N)
Vr    = shear capacity (resisting shear) of masonry, lb (N)

REFERENCES

  1. International Building Code. International Code Council.
    • 2012 Edition
    • 2009 Edition
    • 2006 Edition
  2. Building Code Requirements for Masonry Structures. Reported by the Masonry Standards Joint Committee.
    • 2011 Edition: TMS 402-11/ACI 530-11/ASCE 5-11
    • 2008 Edition: TMS 402-08 /ACI 530-08/ASCE 5-08
    • 2005 Edition: ACI 530-05/ASCE 5-05/TMS 402-05
  3. Allowable Stress Design Tables for Reinforced Concrete Masonry Walls, TEK 14-19B. Concrete Masonry & Hardscapes Association, 2009.
  4. Allowable Stress Design of Concrete Masonry Based on the 2012 IBC & 2011 MSJC, TEK 14-07C. Concrete Masonry & Hardscapes Association, 2011.

 

Allowable Stress Design of Pier and Panel Highway Sound Barrier Walls

  • August 2018

INTRODUCTION

Sound barrier walls are increasingly being used to reduce the impact of traffic noise on properties abutting major urban traffic routes. Because concrete masonry possesses many desirable features and properties—excellent sound resistance, low cost, design flexibility, structural capability and durability, it is an excellent material for the design and construction of highway sound barrier walls.

Aesthetics is also an important consideration. Noise barriers significantly impact a highway’s visual impression. Visual qualities of noise barriers include overall shape, end conditions, color, texture, plantings and artistic treatment.

The variety of concrete masonry surface textures, colors and patterns has led to its extensive use in sound barrier walls.

Various types of concrete masonry walls may be used for sound barriers. Pier and panel walls are relatively easy to build and are economical due to the reduced thickness of the walls and the intermittent pier foundations. In addition, the piers can be offset with respect to the panels to achieve desired aesthetic effects. Pier and panel walls are also easily adapted to varying terrain conditions and are often used in areas that have expansive soils.

This TEK presents information on the structural design of concrete masonry pier and panel sound barrier walls. Requirements and considerations for reduction of highway traffic noise are discussed in TEK 13-03A, Concrete Masonry Highway Noise Barriers (ref. 2).

DESIGN

Building Code Requirements for Masonry Structures, ACI 530/ASCE 5/TMS 402 (ref. 1) includes requirements for allowable stress design, strength design and prestressed approaches. The allowable stress design approach was used to develop the designs in this TEK. Allowable stresses were increased by one-third, as permitted for load combinations which include wind or seismic loads. Allowable Stress Design of Concrete Masonry, TEK 14-07C (ref. 4), describes the basic design approach.

Materials and Workmanship

Since concrete masonry sound barrier walls are subject to a wide range of load conditions, temperatures and moisture conditions, the selection of proper materials and proper workmanship is very important to ensure durability and satisfactory structural performance. Accordingly, it is recommended that materials (concrete masonry units, mortar, grout and reinforcement) comply with applicable requirements contained in Building Code Requirements for Masonry Structures (ref. 1).

Lateral Loads

Design lateral loads should be in accordance with those specified by local or state building and highway departments. If design lateral loads are not specified, it is recommended that they conform to those specified in Minimum Design Loads for Buildings and Other Structures, ASCE 7 (ref. 3). Wind and earthquake loads required in this standard are briefly described in the following paragraphs.

Design wind loads (F) on sound barrier walls may be determined as follows:

For the wall designs in this TEK, G is taken as 0.85 and C as 1.2. The minimum wind load specified in ASCE 7 is f 10 psf (479 Pa). For basic wind speeds of 85 mph (minimum), 90 mph, 100 mph, and 110 mph (53, 145, 161, and 177 kmph), the corresponding wind loads are listed in Table 1.

Earthquake loads (F ) on sound barrier walls may be p determined as follows, considering the wall system as a reinforced masonry non-building structure (ref. 3):

Seismic loads for a range of conditions are listed in Table 3.

Table 1—Wind Loads for Sound Barrier Walls
Table 2— Design Assumptions for Tables 4, 5, and 6
Table 2—Seismic Loads for Sound Barrier Walls

Deflections

Deflection considerations typically govern wall design for long spans and taller walls with greater lateral loads. Deflections are imposed to limit the development of vertical flexure cracks within the wall panel and horizontal flexure cracks near the base of the pier. The design information presented in this TEK is based on a maximum allowable deflection of L/240, where L is the wall span between piers.

DESIGN TABLES

Design information for pier and panel walls is presented in Tables 4 through 7. Tables 4 and 5 provide horizontal reinforcing steel requirements for 6 in. and 8 in. (152 and 203 mm) panels, respectively. Horizontal reinforcement requirements can be met using either joint reinforcement or bond beams with reinforcing bars.

Table 6 provides pier size and reinforcement requirements for various lateral loads. Table 7 lists minimum sizes for pier foundations, as well as minimum embedment depths. These components of pier and panel walls are illustrated in Figure 1.

When pier and panels are used, walls are considered as deep beams, spanning horizontally between piers. Walls support their own weight, vertically, and also must resist lateral out-of-plane wind or seismic loads. The panels are built to be independent of the piers to accommodate masonry unit shrinkage and soil movement. For this design condition, wall reinforcement is located either in the horizontal bed joints or in bond beams. Wall reinforcement is based on maximum moments (M) and shears (V) in the wall panels, determined as follows:

The wall panels themselves are analyzed as simply supported beams, spanning from pier to pier.

In addition to the horizontal reinforcement, which transfers lateral loads to the piers, vertical reinforcement in the panels is required in Seismic Design Categories (SDC) C, D, E and F. Building Code Requirements for Masonry Structures (ref. 1) includes minimum prescriptive reinforcement as follows. In SDC C, vertical No. 4 (M #13) bars are located within 8 in. (203 mm) of the wall ends, and at 10 ft (3.0 m) on center along the length of the wall; minimum horizontal reinforcement requirements are satisfied by the primary reinforcement listed in Tables 4 and 5. In SDC D, E and F, vertical No. 4 (M #13) bars are located within 8 in. (203 mm) of the wall ends, and at 4 ft (1.22 m) on center along the length of the wall.

Table 6 shows pier size and vertical reinforcement requirements. Piers are designed as vertical cantilevers, not bonded with the walls, and pier reinforcement is based on maximum moment and shear, determined as follows:

Design assumptions for the pier and panel walls are given in Table 2. Note that allowable stresses were increased by one-third, as permitted for load combinations which include wind or seismic loads (ref. 1).

Requirements for concrete foundations supporting the concrete masonry piers are given in Table 7. These foundations can be constructed economically by drilling. The concrete foundation piers should contain vertical reinforcement (same as shown in Table 6) which should be properly lapped with vertical reinforcement in the concrete masonry piers. The embedment depths given in Table 7 are based on an allowable lateral passive soil pressure of 300 psf (14.4 kPa).

Table 4—6 in. (152 mm) Panel Wall Reinforcement
Table 5—8 in. (203 mm) Panel Wall Reinforcement
Table 6—Pier Size and Reinforcement
Table 7—Pier Foundation Requirements, Minimum Embedment/Diameter

DESIGN EXAMPLE

A pier and panel highway sound barrier is to be designed using the following parameters:

  • 6 in. (152 mm) panel thickness
  • 10 ft (3.05 m) wall height
  • 14 ft (4.27 m) wall span
  • open terrain, stiff soil
  • basic wind speed is 90 mph (145 km/h)
  • SS = 0.25, SDC B

From Table 1, the design wind load is 14.1 psf (674 Pa) for a basic wind speed of 90 mph (145 km/h) and exposure C. Using Table 3, the design seismic load is determined to be 2.8 psf (0.13 kPa) for a 6 in. (152 mm) wall grouted at 48 in. (1219 mm), or less, on center, for SS = 0.25. Since the wind load is s greater, the wall will be designed for 14.1 psf (674 Pa).

Using Table 4, minimum horizontal panel reinforcement is either W1.7 (MW 11) joint reinforcement at 8 in. (203 mm) on center, or bond beams at 48 in. (1220 mm) on center reinforced with one No. 5 (M #16) bar. At the bottom, the panel requires a beam 16 in. (406 mm), or two courses, deep reinforced with one No. 5 (M # 16) bar (last column of Table 4). Because the wall is located in SDC B, vertical reinforcement is not required to meet prescriptive seismic requirements.

The minimum pier size is 16 x 18 in. (406 x 460 mm), reinforced with four No. 4 (M #13) bars, per Table 6. The pier foundation diameter is 18 in. (457 mm), and should be embedded at least 7.5 ft (2.29 m), per Table 7.

NOTATIONS

Af    = area normal to wind direction, ft² (m²)
Cf    = force coefficient (see ref. 3)
d     = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
Em  = modulus of elasticity of masonry in compression, psi (MPa)
Es   = modulus of elasticity of steel, psi (MPa)
F     = design wind load, psf (Pa) (see ref. 3)
Fa   = acceleration-based site factor (at 0.3 second period) (see ref. 3)
Fm  = allowable masonry flexural compression stress, psi (Pa)
Fp   = seismic force, psf (Pa) (see ref. 3)
Fs   = allowable tensile or compressive stress in reinforcement, psi (MPa)
Fv   = allowable shear stress in masonry, psi (MPa)
f’m  = specified compressive strength of masonry, psi (MPa)
G    = gust effect factor (see ref. 3)
H    = wall height, ft (m)
I     = importance factor (see ref. 3)
Ip   = component importance factor (assume equal to 1.0 for sound barrier walls) (see ref. 3)
Kd  = wind directionality factor (see ref. 3)
Kz  = velocity pressure exposure coefficient (see ref. 3)
Kzt = hill and escarpment factor (see ref. 3)
L    = wall span, ft (m)
M   = maximum moment at the section under consideration, in.-lb (N-mm)
n    = ratio of elastic moduli, Es/Em
P    = applied lateral force, lb (N)
qz   = velocity pressure, psf (Pa) (see ref. 3)
= 0.00256K KzKztKdv²I
R    = response modification coefficient (see ref. 3)
Rp   = component response modification factor (equal to 3.0 for reinforced masonry non-building structures) (see ref. 3)
SDS = design short period spectral acceleration =⅔(FaSS), where SS varies from less than 0.25 to greater than 1.25, and Fa is dependent on SS and soil conditions at the site (see ref. 3)
Ss    = mapped maximum considered earthquake spectral response acceleration at short periods (see ref. 3)
V     = shear force, lb (N)
v      = basic wind speed, mph (km/h) (see ref. 3)
Wp   = weight of wall, psf (Pa)
w      = wind or seismic load, psf (Pa)

REFERENCES

  1. Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
  2. Concrete Masonry Highway Noise Barriers, TEK 13-03A. Concrete Masonry & Hardscapes Association, 1999.
  3. Minimum Design Loads for Buildings and Other Structures, ASCE 7-02. American Society of Civil Engineers, 2002.
  4. Allowable Stress Design of Concrete Masonry, TEK 14-07C Concrete Masonry & Hardscapes Association, 2002.

 

Loadbearing Concrete Masonry Wall Design

  • August 2018

INTRODUCTION

Structural design of buildings requires a variety of structural loads to be accounted for: dead and live loads, those from wind, earthquake, lateral soil pressure, lateral fluid pressure, as well as forces induced by temperature movements, creep, shrinkage, and differential movements. Because any load can act simultaneously with another, the designer must consider how these various loads interact on the wall. For example, an axial load can offset tension due to lateral load, thereby increasing flexural capacity, and, if acting eccentrically, can also increase the moment on the wall. Building codes dictate which load combinations must be considered, and require that the structure be designed to resist the most severe load combination.

The design aids in this TEK cover combined axial compression or axial tension and flexure, as determined using the allowable stress design provisions of Building Code Requirements for Masonry Structures (ref. 1). The data in this TEK applies to 8 in. (203 mm) thick reinforced concrete masonry walls with a specified compressive strength, f’m, of 1500 psi (10.3 MPa), and a maximum wall height of 20 ft (6.1 m) (taller walls can be evaluated using the NCMA computer software (ref. 3) or other design tools). Reinforcing bars are assumed to be located at the center of the wall, and bar sizes 4, 5, 6, 7, and 8 are included.

AXIAL LOAD-BENDING MOMENT INTERACTION DIAGRAMS

Several design approaches are available for combined axial compression and flexure, most commonly using computer programs to perform the necessary iterative calculations, or using interaction diagrams to graphically determine required reinforcement for the given conditions. Axial load–bending moment interaction diagrams account for the interaction between moment and axial load on the design capacity of a reinforced (or unreinforced) masonry wall.

Figure 1—Full Axial Load-Bending Moment Interaction Diagram (Ref. 2), Dashed Box Indicates Region Displayed In Figures 3 Through 7

Regions of the Interaction Diagram

The various interaction diagram regions are discussed below. Figure 2 shows a typical interaction diagram for a reinforced masonry wall subjected to combined axial load and bending moment. Three distinct regions (I, II and III) can be identified, each with very different characteristics and behavior.

Region I represents the range of conditions corresponding to an uncracked section. That is, there is no tendency for the wall to go into tension, hence the design is governed by masonry compressive strength. Because the Building Code Requirements for Masonry Structures (ref. 1) only permits reinforcing steel to carry an allowable compression stress if it is laterally tied, and since it is generally not practical to do so, the reinforcing steel is simply neglected.

Region II is characterized by cracking in the section, but the reinforcing steel remains subject to compression strain. Hence in Region II, as in Region I, the reinforcing steel is ignored – i.e., the size and location of reinforcing steel are irrelevant. Since the section is cracked, the properties of the cross-section change as the eccentricity changes.

Region III corresponds to values of 0 ≤ k ≤ 1 (tension governs the design). This is the only region where the reinforcing steel affects the capacity of the section.

The load capacity can also be limited by wall slenderness if the eccentricity is sufficiently small and the slenderness sufficiently large. The horizontal line shown in Figure 2 in Region I illustrates the effect of this upper limit on the interaction diagram.

A complete discussion of interaction diagrams, including the governing equations for the various regions, is included in Concrete Masonry Design Tables (ref. 2).

Figure 2—Interaction Diagram of Fully Grouted Reinforced Wall Showing Three Regions

Figures 3 Through 7

Figures 3 through 7 are axial load-bending moment interaction diagrams for reinforcing bar sizes No. 4, 5, 6, 7 and 8, respectively, which can be used to aid in the design of both fully and partially grouted 8 in. (203 mm) single wythe concrete masonry walls. Rather than the full interaction diagram, only the portion outlined by the dashed box in Figure 1 is shown. With reinforcing steel located in the center of the wall, wall strength will be the same under either a positive or negative moment of the same magnitude. Therefore, although negative moments are not shown, the figures may be used for these conditions.

This area of the interaction diagram covers the majority of design applications. Conditions outside of this area may be determined using Concrete Masonry Design Tables (ref. 2). Each line on the diagram represents a different reinforcing bar spacing, included at 8 in. (203 mm) increments.

Building Code Requirements for Masonry Structures (ref. 1) permits a ⅓ increase in allowable stresses when load combinations include wind or seismic loads. Figures 3 through 7 represent load combinations excluding wind or seismic (i.e., no increase in allowable stresses is included). However, these diagrams can be used for load combinations including wind or seismic by multiplying the total applied axial load and moment by 0.75 (see Design Example section).

These interaction diagrams also conform to the International Building Code (ref. 4) basic load combinations for allowable stress design (not including 1/3 stress increase for for wind or seismic). A stress increase is allowed under the IBC alternative basic load combinations but is applied in a different manner than in MSJC. Therefore, the IBC 1/3 stress increase cannot be used in conjunction with these tables.

Figure 3—Interaction Diagram of 8 in. (203 mm) Concrete Masonry Wall With No. 4 Reinforcing Bars
Figure 4—Interaction Diagram of 8 in. (203 mm) Concrete Masonry Wall With No. 5 Reinforcing Bars
Figure 5—Interaction Diagram of 8 in. (203 mm) Concrete Masonry Wall With No. 6 Reinforcing Bars
Figure 6—Interaction Diagram of 8 in. (203 mm) Concrete Masonry Wall With No. 7 Reinforcing Bars
Figure 7—Interaction Diagram of 8 in. (203 mm) Concrete Masonry Wall With No. 8 Reinforcing Bars

DESIGN EXAMPLE – LOADBEARING WALL

A 20 ft (6.1 m) high reinforced concrete masonry wall is to be designed to resist wind load as well as eccentrically applied axial live and dead loads as depicted in Figure 8. The designer must determine the reinforcement size and spacing required to resist the applied loads, listed below.

D = 520 lb/ft (7.6 kN/m), at e = 0.75 in. (19 mm)
L = 250 lb/ft (3.6 kN/m), at e = 0.75 in. (19 mm)
W = 20 psf (1.0 kPa)

The maximum moment due to the wind load is determined as follows.

The axial load used for design is the axial load at the location of maximum moment. This combination may not necessarily be the most critical section for combined axial load and flexure, but should be close to the critical location. The wall weight is estimated to be halfway between fully grouted and hollow (82 and 38.7 psf (400 and 189 kg/m²), respectively, for 115 pcf (1842 kg/m³) unit concrete density).

The eccentricity of the axial loads also induces bending in the wall and should be included in the applied moment. The magnitude of the moment due to the eccentric axial load must be found at the same location as the maximum moment.

The induced bending moments due to the eccentric axial loads are insignificant compared to that due to wind. However, these will be taken into account where appropriate for specific load combinations.

The applicable load combinations (ref. 1) for this example are:

D + L
D + L + W
D + W

During design, all three load combinations should be checked, with the controlling load case used for design. For brevity, only the third combination (D + W) will be evaluated here, since the axial load actually increases the flexural capacity for the first two combinations by offsetting tension in the wall due to the lateral load. Because the interaction diagrams in this TEK are for load combinations excluding wind or seismic, the total moment, shear and axial loads the wall must resist (listed below) are multiplied by 0.75 to account for the ⅓ increase in allowable stresses permitted by section 2.1.1.1.3 in Building Code Requirements for Masonry Structures (ref. 1).

To determine the required reinforcement size and spacing to resist these loads, P10’ and Mmax are plotted on the appropriate interaction diagram(s) until a satisfactory design is found.

Figure 3 shows that No. 4 bars at 32 in. (813 mm) on center are adequate. If a larger bar spacing is desired, No. 5 bars at 48 in. (1219 mm) on center will also meet the design requirements (see Figure 4). Although wall design is seldom governed by out-of-plane shear, the shear capacity should be checked. In addition, the axial load should be recalculated based on the actual wall weight (based on grout spacing chosen), then the resulting required capacity should be recalculated and plotted on the interaction diagram to check adequacy.

Figure 8—Wall Section for Loadbearing Wall Design Example

NOMENCLATURE

An    net cross sectional area of masonry, in.²/ft (mm²/m)
D     dead load, lb/ft (kN/m)
d      distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
e       eccentricity of axial load – measured from centroid of masonry unit, in. (mm)
Fa     allowable compressive stress due to axial load only, psi (MPa)
Fb     allowable masonry compressive stress due to flexure only, psi (MPa)
Fs      allowable steel tensile stress, psi (MPa)
fy       yield stress of steel, psi (MPa)
f’m     specified masonry compressive strength, psi (MPa)
H       height of wall, ft (m)
k        ratio of the distance between compression face of wall and neutral axis to the effective depth, d
L        live load, lb/ft (kN/m)
M       moment acting on section, in.-lb/ft or ft-lb/ft (kN m/m)
P        axial force or concentrated load, lb/ft (kN/m)
Pb       axial force corresponding to balanced condition, lb (kN)
Po       maximum axial force ordinate on interaction diagram, lb (kN)
s          reinforcement spacing, in. (mm)
t          thickness of masonry, in. (mm)
tnom   nominal wall thickness, in. (mm)
V        shear acting at a section, lb/ft (kN/m)
W       wind load, psf (kN/m²)
y         distance measured from top of wall, ft (m)

METRIC CONVERSIONS

To convert:To metric units:Multiply English units by:
ftm0.3048
ft-lb/ftN m/m4.44822
in.mm25.4
lb/ftN/m14.5939
psiMPa0.00689476

REFERENCES

  1. Building Code Requirements for Masonry Structures, ACI 530/ASCE 5/TMS 402. Reported by the Masonry Standards Joint Committee, 1999/2002/2005.
  2. International Building Code. International Codes Council, Falls Church, VA, 2000/2003/2006.

Designing Concrete Masonry Walls for Wind Loads

  • August 2018

INTRODUCTION

Traditionally, empirical requirements have been used for the selection of masonry wall dimensions and lateral support spacing for resistance to wind pressures. These empirical requirements provide satisfactory results for buildings less than 35 ft (11 m) in height where the basic wind pressure does not exceed 25 psf (1197 Pa). This TEK addresses those cases where it is necessary or desirable to undertake a more thorough structural analysis of the lateral wind resistance of a concrete masonry wall or wall-pilaster combination.

Such analysis involves a knowledge of the magnitude and distribution of the wind force to various elements of a masonry structure and the flexural and shear strength of these elements. The information in this TEK provides guidelines for the design of masonry walls supported in both the vertical and horizontal directions.

WALLS

The need to investigate the lateral wind resistance capacity of a wall is usually greater in the case of plain (unreinforced) nonbearing or lightly loaded masonry walls because the vertical load on the wall may be insufficient to completely offset the development of flexural tension. Analysis of masonry walls is often based on the assumption that lateral loads are transmitted in the vertical direction with no end fixity at the lateral supports. Although this approach is straightforward, it may be overly conservative when the ratio of horizontal to vertical distances between lateral supports is relatively small and end fixity is developed. In such cases, end fixity and two-way bending can be utilized.

When wind loads are applied normal to a masonry wall surface, the loads are transmitted to horizontal supports (floors, roofs, beams) and/or vertical supports (cross walls, pilasters). Wall panels are usually assumed to function structurally as thin plates or slabs. For simplicity, walls are often designed to span horizontally between vertical supports or to span vertically between horizontal supports. However, walls can be designed assuming two-way bending using pilasters or cross walls as well as the roof structure and footing as supports. Assuming that the flexural resistance and rigidity of the walls in both the vertical and horizontal spans are known, the lateral load capacity and the proportion of the lateral load transmitted vertically and horizontally to the edge supports will depend on the restraint developed at the edges, the horizontal to vertical span ratio of the panel, and the distribution of the loads applied to the wall panels.

The curves in Figure 1 can be used to approximate the proportion of wind load transmitted in the vertical and horizontal directions. These curves are based on the assumption that the moment of inertia and modulii of elasticity of the walls will be the same in both the horizontal and vertical directions. The curves were derived by equating the theoretical formulas for calculating the maximum deflection for a strip of wall in both directions. It was further assumed that the walls either have no openings, or that any wall openings are located so that their effect on the stiffness of the wall panel is the same in both directions, and that the wall panels on each side of the support are similar in length and height.

When calculating the wind load to be carried by a vertical support, such as a pilaster, a value for K corresponding to the assumed support conditions at the edges of the wall panels and the appropriate wall panel length-to-height ratio is selected from the curves. Then, the value of wp is determined from the formula given at the top of Figure 1. This value, wp, represents the load which, when applied as a uniformly distributed load over the height of the pilaster, will approximate the actual wind load transmitted to the pilaster by the walls under the design conditions.

Figure 1—Approximate Horizontal and Vertical Wind Load Distribution

Design Example

To illustrate the use of the curves and formula given in Figure 1, assume a building with exterior walls spanning 12 ft (3.7 m) vertically between the floor and the roof is designed to resist a wind pressure of 20 psf (958 Pa). The walls are also supported horizontally at 18 ft (5.5 m) by pilasters which are built integrally with the wall. The roof loads will be carried by trusses simply supported on the pilasters, so the walls will be considered free at the top and fixed at the bottom and at the pilasters.

Selecting the appropriate value for K from the curve given for Case 1-A and a wall length-to-height ratio of 18/12 or 1.50, the wind load per foot of height to be carried by the pilasters, wp, may be calculated as follows:

wp =Kwd X
wp = (0.91) (20 psf) (18 ft)
= 328 lb/ft (4787 N/m)

The value of 328 lb/ft (4787 N/m) represents the uniformly distributed load which, when considered to be applied over the full height of the pilaster, will approximate the actual load transmitted to the pilasters by the adjacent walls under the design conditions. The moment and shear developed in the pilasters as a result of this load will depend on the assumed top and bottom support conditions for the pilaster.

The wall construction consists of 12 in. (305 mm) hollow concrete masonry units laid in running bond with face shell mortar bedding, using Type N portland cement lime mortar. Additional design information includes:

Section modulus, S = 159.9 in.³/ft (0.009 m³/m)
Net area, An = 36 in.²/ft (0.08 m²/m)
Allowable tensile stress parallel to bed joints = 1.33 x 38 psi = 50.5 psi (0.35 MPa) (ref. 1)
Allowable tensile stress normal to bed joints = 1.33 x 19 psi = 25.3 psi (0.17 MPa) (ref. 1)

As already determined, the horizontal span carries 91% of the wind load. With the wall fixed at the ends, the maximum moment, M, in the horizontal span (from Figure 2) is:

The flexural tensile stress in the horizontal span, ft, is:

The allowable tensile stress for hollow units, Type N mortar, tension parallel to bed joints, was determined to be 50.5 psi (0.35 MPa). Since the calculated tensile stress is less than the allowable, the design meets the code criteria.

In the vertical span, the wall described above carries 9% (1 – 0.91) of the wind load. Since the wall is free at the top and fixed at the base, the maximum moment is:

The flexural tensile stress in the vertical span is:

This value can be reduced by the dead load stress on the wall at the point of maximum moment. Assuming that the wall weighs 50 lb/ft² (2394 N/m²):

This results in a net axial compressive stress of 7 psi (48.3 Pa).

PILASTERS

A pilaster is a thickened wall section or vertical support built contiguous with and forming a part of the masonry wall. Pilasters are often used to stiffen masonry walls and to provide all or part of the lateral support. They may be built of hollow or solid units (manufactured in one or two pieces), grouted hollow units or reinforced hollow units. Pilasters function primarily as flexural members when used only for lateral support although they can also be used to support vertical compressive loads.

When designing pilasters, the lateral loads transmitted to the pilasters by the adjacent wall panels must be determined. Figure 1 can be used to approximate the proportion of wind load which is transmitted horizontally to pilasters and to calculate the approximate wind load carried by a pilaster.

The formulas given in Figure 2 can be used to calculate the maximum moment and shear on a pilaster after wp and the support conditions for the pilaster have been determined.

Consider the design described in the previous design example. From Figure 1, it was determined that for Case 1-A with span ratio of 1.5, approximately 91% of the wind load is transmitted in the horizontal span. If the pilasters in the above example are assumed to be fixed at the bottom and simply supported at the top, the maximum moment and shear values are as follows:

The pilaster, therefore, should be designed to provide an allowable moment and shear resistance equal to or greater than the above values.

Figure 2—Formulas For Maximum Moment and Shear on Walls and Pilasters Subjected To Uniform Lateral Loads

NOTATION:

An     = net cross-sectional area of masonry, in.²/ft (m²/m)
ft       = flexural tension in masonry, psi (MPa)
H      = height of wall, ft (m)
K       = proportion of wind load transmitted horizontally to pilasters or cross walls
M      = moment, in.-lb/ft (N•m/m)
S        = section modulus, in.³/ft (m³/m)
Vmax = maximum shear, lb/ft (N/m)
w       = uniformly distributed wind load, psf (Pa)
wd     = design wind load on wall, psf (Pa)
wp     = uniform lateral load which approximates the actual wind load transmitted by the walls to the pilasters or cross walls, lb/ft of height (N/m)
X       = horizontal span of wall, from center to center of pilasters or cross walls, ft (m)

REFERENCES

  1. Building Code Requirements for Masonry Structures, ACI 530-92/ASCE 5-92/TMS 402-92. Reported by the Masonry Standards Joint Committee, 1992.

TEK 14-03A, Revised 1995.

Splices, Development & Standard Hooks for Concrete Masonry Based on the 2009 & 2012 IBC

  • August 2018

INTRODUCTION

Building codes include requirements for minimum reinforcement development lengths and splice lengths, as well as requirements for standard hooks, to ensure the adequate transfer of stresses between the reinforcement and the masonry. This TEK presents these requirements, based on the provisions of both the 2012 and 2009 editions of the International Building Code (IBC) (refs. 1, 2). Masonry design in these codes is primarily based on Building Code Requirements for Masonry Structures (MSJC) (refs. 3, 4). Differences between the MSJC and IBC are noted in the text when they occur.

There are two main differences between the 2008 and 2011 editions of the MSJC that impact reinforcement development and splice lengths in the corresponding 2009 and 2012 editions of the IBC:

  1. under 2011 MSJC allowable stress design, the allowable tensile stress, Fs, of Grade 60 steel was increased from 24,000 psi (166 MPa) to 32,000 psi (221 MPa), and
  2. the 2011 MSJC includes new lap splice length provisions for when confinement reinforcement is used at lap splices.

TEK 12-04D (ref. 5) includes basic material requirements, corrosion protection and placement tolerances for reinforcement used in concrete masonry construction. In addition, prestressing steel is discussed in Post-Tensioned Concrete Masonry Wall Construction, TEK 03-14 (ref. 6).

SPLICES AND DEVELOPMENT LENGTH

Minimum development lengths are necessary to adequately transfer stresses between reinforcement and the grout or mortar in which it is embedded. Splicing of reinforcement serves a similar purpose: to adequately transfer stresses from one reinforcing bar to another.

Reinforcement can be developed by embedment length, hook, or mechanical anchoring device. The development of the reinforcing bars relies on mechanical interlock of the bar deformations, hook, and/or anchor along with sufficient masonry cover to prevent splitting of the masonry. Reinforcing bars may be spliced by lapping the reinforcement, by proprietary mechanical splices or by welding.

The required length of lap or development is determined according to the design procedure used (allowable stress design or strength design). In addition, these detailing requirements have been frequently revised in recent years. As a result, the minimum lap and development lengths can vary considerably from one code to the next as well as from one design method to another.

The following sections present the requirements for both the 2009 IBC and 2012 IBC for both allowable stress and strength design.

2009 IBC SPLICE & DEVELOPMENT REQUIREMENTS

2009 IBC Allowable Stress Design

Development Length & Lap Splicing

While the 2008 MSJC includes an equation to determine development and lap splice lengths, the 2009 IBC modifies the MSJC lap splice length. In accordance with the 2009 IBC, the minimum required lap length for spliced reinforcing bars is determined using Equation 1 (see Table 1).

but not less than 12 in. (305 mm) or 40db, whichever b is greater

Further, in regions of flexure where the design tensile stresses in the reinforcement, fs, exceed 80% of the allowable steel tensile stress, Fs, the IBC requires that the required length of lap determined by Equation 1 must be increased by 50%. Alternatively, equivalent means of stress transfer to accomplish the same 50% increase is permitted. Where epoxy coated bars are used, lap length is also required to be increased by 50% but does not apply to the 12 in. (305 mm) minimum.

Development length requirements for allowable stress design are determined in accordance with Equation 3 except that there is no maximum length limit of 72db.

When noncontact lap splices are used, the bars must be spaced no farther apart than one-fifth the required length of lap nor more than 8 in. (203 mm).

When using the allowable stress design method, development of wires in tension is determined using Equation 2 (see Table 2). The development length of epoxy-coated wires is increased 50% above the value determined using Equation 2 but does not apply to the 6 in. (152 mm) minimum.

but not less than 6 in. (152 mm)

Table 1—2009 IBC Allowable Stress Design Lap Splice Lengths (ref. 2)
Table 2—2009 & 2012 IBC Allowable Stress Design Development Lengths for Wire (refs. 1, 2) (A)

A See Equation 2. fs = 30,000 psi (207 MPa). Lap splice length not less than 6 in. (152 mm). Increase development lengths by 50% when epoxy coated wire is used, but this increase does not apply to the 6 in. (152 mm) minimum..

Alternatives to Lap Splicing

Reinforcing bars can also be spliced by welding, mechanical splicing and in some cases end-bearing splicing. Reinforcing bars larger than No. 9 (M#29) are required to be spliced using mechanical connectors.

Welded splices require the bars to be butted or shortly lapped and welded to develop in tension at least 125% of the specified yield strength of the bar. All welding is required to conform to AWS D1.4 (ref. 7), and steel for welded splices must conform to ASTM A706 (ref. 8). In practice, however, welding tends to be an expensive splicing option.

Mechanical splicing of reinforcement typically employs proprietary couplers specifically designed for this application. Mechanical splices are required to have the bars connected to develop in tension or compression, as required, at least 125% of the specified yield strength of the bar.

Reinforcing bars can also be spliced using end-bearing splices, but only in members containing closed ties, closed stirrups or spirals for bars subject to compression only. End-bearing splices rely on the transmission of compressive stress by bearing of square-cut ends held in concentric contact by a suitable device. The bar ends are required to terminate in flat surfaces within 11/2 degrees of a right angle to the axis of the bars and be fitted within 3 degrees of full bearing after assembly. 

2009 IBC Strength Design

Development Length & Lap Splice Length

For development and lap splice length requirements, the 2009 IBC references the 2008 MSJC (see Equation 3 and Table 3), but adds a maximum length limit of 72db.

For Equation 3, the reinforcement size factor, g, is taken equal to 1.0 for No. 3 through No. 5 (M#10–M#16) reinforcing bars; 1.3 for No. 6 and No. 7 (M#19, M#22) bars; and 1.5 for No. 8 and No. 9 (M#25, M#29) bars. When epoxy coated bars are used, the development length determined by Equation 3 is required to be increased by 50%.

Bars spliced by noncontact lap splices must be spaced no farther apart than one-fifth the required length of lap and no more than 8 in. (203 mm).

Alternatives to Lap Splicing

Mechanical splices are required to have the bars connected to develop at least 125% of the specified yield strength of the bar in tension or compression, as required.

The IBC further stipulates that mechanical splices be classified as Type 1 or 2 according to Section 21.2.6.1 of ACI 318, Building Code Requirements for Structural Concrete and Commentary (ref. 10). Type 1 splices may not be used within the plastic hinge zone nor within a beam-column joint of intermediate or special reinforced masonry shear walls or special moment frames. Type 2 are permitted at any location.

A Type 2 splice is defined as a full mechanical splice that develops in tension or compression, as required, at least 1.25fy of the bar. This requirement is intended to avoid a splice failure when the reinforcement is subjected to expected stress levels in yielding regions. Type 1 splices are not required to satisfy the more stringent requirements for Type 2 splices, and so their use is limited as noted above.

Welded splices must have the bars butted and welded to develop at least 125% of the bar’s specified yield strength in tension or compression, as required. Welded splices must use ASTM A706 (ref. 9) steel reinforcement. Welded splices are not permitted to be used in plastic hinge zones of intermediate or special reinforced walls nor in special moment frames of masonry.

2012 IBC SPLICE & DEVELOPMENT REQUIREMENTS

Regarding development and splice lengths, two significant changes were incorporated into the 2011 MSJC, which are included by reference in the 2012 IBC:

  1. in the 2011 MSJC, the allowable tensile stress, Fs, of Grade 60 steel when using allowable stress design was increased from 24,000 psi (166 MPa) to 32,000 psi (221 MPa), and
  2. the 2011 MSJC includes new provisions for confinement reinforcement, for both allowable stress and strength design methods.

2012 IBC Allowable Stress Design

Equation 1 is still applicable for use in the 2012 IBC but with the increase in F the splice lengths of fully stressed bars will increase by 33%. Significant reductions of splice lengths in low stress areas are achieved, however. The minimums of 12 in. (305 mm) or 40db whichever is greater still apply as well.

The 2012 IBC allows the MSJC development length equation (Equation 3) to be used as an alternate to the IBC equation (Equation 1). When using Equation 3 under the 2012 IBC, however, the value of K is defined as the least of the masonry cover, 9db (vs. 5db in the 2009 IBC) and the clear spacing between adjacent reinforcement.

Tabulated values are presented in Tables 4a through 4d. Note, however, that there is no maximum length limit of 72db for allowable stress design.

Tables 4a and 4b present minimum lap splice lengths for reinforcement placed in the center of the wall, for f’m = 1,500 and 2,000 psi (10.3 and 13.7 MPa), respectively.

Tables 4c and 4d present minimum lap splice lengths for reinforcement offset in the wall, for f’m = 1,500 and 2,000 psi (10.3 and 13.7 MPa), respectively.

Other requirements for lap, mechanical, welded and end-bearing splices are identical to those under the 2009 IBC, with the exception of the new provisions for confinement reinforcement, presented below.

2012 IBC Strength Design

Requirements for development length as well as lap, mechanical and welded splices are identical to those for allowable stress design, and are presented in Tables 4a through 4d.

2012 IBC Lap Splices With Confinement Reinforcement

The 2012 IBC, by reference to the 2011 MSJC, includes new lap splice criteria where confinement reinforcement is placed. The criteria are the same for both allowable stress design and strength design.

The confinement reinforcement criteria allow a reduced lap splice length when reinforcement is provided transverse to lapped bars. Research has found that the transverse, or confinement, reinforcement increases the lap performance significantly, as long as there is at least one No. 3 (M#10) or larger transverse bar placed within the last 8 in. (203 mm) of each end of the lap (see Figure 1). Because of this effect, calculated lap splice lengths are permitted to be reduced by a confinement factor, ξ, determined using Equation 4:

where

db is the bar diameter of the vertical reinforcement

The reduced lap splice length is not permitted to be less than 36db. The clear space between the transverse bars and the lapped bars may not exceed 1.5 in. (38 mm), and the transverse bars must be fully developed in grouted masonry at the point where they cross the lapped reinforcement (see Figure 1). These provisions are included in Tables 4a through 4d

Table 3—2009 IBC Strength Design Lap Splice Lengths (ref. 2)A
Figure 1—Confinement Reinforcement at Lap Splice
Table 4a—2012 IBC Lap Splice Lengths, f’m = 1,500 psi (10.3 MPa), Reinforcement in Center of Wall (ref. 1)A
Table 4b—2012 IBC Lap Splice Lengths, f’m = 2,000 psi (13.7 MPa), Reinforcement in Center of Wall (ref. 1)A
Table 4c—2012 IBC Lap Splice Lengths, f’m = 1,500 psi (10.3 MPa), Reinforcement Off-Center (ref. 1)A
Table 4d—2012 IBC Lap Splice Lengths, f’m = 2,000 psi (13.7 MPa), Reinforcement Off-Center (ref. 1)A

STANDARD HOOKS

Figure 2 illustrates the requirements for standard hooks, when reinforcing bars are anchored by hooks or by a combination of hooks and development length. These requirements apply to both the 2009 and 2012 IBC, for both allowable stress and strength design. Table 5 lists minimum dimensions and equivalent embedment lengths for standard hooks of various sizes. A combination of hook and development length must be used when the equivalent embedment length of the hook, le, is less than the required minimum development length, ld. In this case, development length equal to (ld – le) must be provided in addition to the hook. This additional development length is measured from the start of the hook (point of tangency with the main portion of the bar).

Figure 2—Standard Hooks
Table 5—Standard Hooks—Dimensions and Equivalent Embedment Lengths

JOINT REINFORCEMENT SPLICES

Joint reinforcement must have a minimum splice length of 6 in. (152 mm) to transfer shrinkage stresses. Slippage of the deformed side wires is resisted by surface bond as well as by mechanical anchorage of the embedded portions of the cross wires.

NOTATIONS:

Asc = area of the transverse bars at each end of the lap splice, in.² (mm²)
Di = min. inside diameter of bend for standard hooks, in. (mm)
db = nominal diameter of reinforcement, in. (mm)
K = the least of the masonry cover, 9db for the 2012 IBC (5db for the 2009 IBC) and the clear spacing between adjacent reinforcement, in. (mm)
Fs = allowable tensile stress in reinforcement, psi (MPa)
f’m = specified compressive strength of masonry, psi (MPa)
fs = calculated tensile or compressive stress in steel, psi (MPa)
fy = specified yield strength of steel, psi (MPa)
ld = embedment length or lap splice length of straight reinforcement, in. (mm)
le = equivalent embedment length provided by standard hooks measured from the start of the hook (point of tangency), in. (mm)
lt = length of bar extension of hooked confinement reinforcement, in. (mm)
γ = reinforcement size factor
ξ = lap splice confinement reinforcement factor

REFERENCES

  1. International Building Code 2012. International Code Council, 2012.
  2. International Building Code 2009. International Code Council, 2009.
  3. Building Code Requirements for Masonry Structures, TMS 402-11 /ACI 530-11/ASCE 5-11. Reported by the Masonry Standards Joint Committee, 2011.
  4. Building Code Requirements for Masonry Structures, TMS 402-08 /ACI 530-08/ASCE 5-08. Reported by the Masonry Standards Joint Committee, 2008.
  5. Steel Reinforcement for Concrete Masonry, TEK 12-04D. Concrete Masonry & Hardscapes Association, 2007.
  6. Post-Tensioned Concrete Masonry Wall Construction, TEK 03-14. Concrete Masonry & Hardscapes Association, 2002.
  7. Structural Welding Code—Reinforcing Steel, AWS D 1.4-05. American Welding Society, 2005.
  8. Standard Specification for Low-Alloy Steel Deformed and Plain Bars for Concrete Reinforcement, ASTM A706/A706M-09b. ASTM International, Inc., 2009.
  9. Building Code Requirements for Structural Concrete and Commentary, ACI 318-11. American Concrete Institute, 2011.

TEK 12-06A, Revised 2013. CMHA and the companies disseminating this technical information disclaim any and all responsibility and liability for the accuracy and the application of the information contained in this publication.

Design of Anchor Bolts Embedded in Concrete Masonry

  • August 2018

INTRODUCTION

The function of anchor bolts is to transfer loads to the masonry from attachments such as ledgers, sills, and bearing plates. Both shear and tension are transferred through anchor bolts to resist design forces such as uplift due to wind at the top of a column or wall or vertical gravity loads on ledgers supporting joists or trusses (see Figure 1). The magnitude of these loads varies significantly with the application.

This TEK summarizes the requirements to properly design, detail and install anchor bolts embedded in concrete masonry construction based on the provisions of the 2013 edition of Building Code Requirements for Masonry Structures (ref. 1). It should be noted that the 2012 editions of the International Building Code and International Residential Code (refs. 3 and 4) reference the provisions of the 2011 edition of Building Code Requirements for Masonry Structures (ref. 5) which contain no significant differences from the following analysis and design methodologies.

Anchor bolt configurations covered by Building Code Requirements for Masonry Structures fall into one of two categories:

• Bent-bar anchors, which include the customary J and L bolts, are threaded steel rods with hooks on the end embedded into the masonry. Bent-bar anchor bolts must meet the material requirements of Standard Specification for Carbon Structural Steel, ASTM A36/A36M (ref. 6).

• Headed anchors include conventional square head or hexhead threaded bolts, but also include plate anchors (where a steel plate is welded to the end of the bolt). Headed anchor bolts must meet the requirements of Standard Specification for Carbon Steel Bolts and Studs, 60,000 psi Tensile Strength, ASTM A307, Grade A (ref. 7).

For other anchor bolt configurations, including post-installed anchors, design loads are determined from testing a minimum of five specimens in accordance with Standard Test Methods for Strength of Anchors in Concrete and Masonry Elements, ASTM E488 (ref. 8) under stresses and conditions that represent the intended use. Allowable stress design values are limited to 20% of the average tested anchor bolt strength. Using strength design provisions, nominal design strengths are limited to 65% of the average tested strength.

Figure 1—Anchorage Design Loads

GENERAL DESIGN AND DETAILING REQUIREMENTS

Building Code Requirements for Masonry Structures (ref. 1) contains anchor bolt design provisions for both the allowable stress design and strength design methods (Chapters 2 and 3, respectively). An overview of these design philosophies can be found in Allowable Stress Design of Concrete Masonry, TEK 14-07C, and Strength Design Provisions for Concrete Masonry, TEK 14-04B (refs. 9, 10). Note that Chapter 5 of the code also includes prescriptive criteria for floor and roof anchorage that are applicable to empirically designed masonry, but these provisions are not covered here.

While many of the requirements for anchor design vary between the allowable stress and strength design methods, some provisions are commonly shared between the two design approaches. The following discussion and topics apply to anchors designed by either the allowable stress or strength design methods.

Effective Area of Anchor Bolts

For both design methods, the anchor bolt net area used to determine the design values presented in this TEK are taken equal to the following, which account for the reduction in area due to the presence of the anchor threading:

½ in. anchor = 0.142 in.² (91.6 mm²)
⅝ in. anchor = 0.226 in.² (145.8 mm²)
¾ in. anchor = 0.334 in.² (215.4 mm²)
⅞ in. anchor = 0.462 in.² (298.0 mm²)

Effective Embedment Length

The minimum effective embedment length for anchor bolts is four bolt diameters (4db) or 2 in. (51 mm), whichever is greater (see Figure 2). The embedment length of headed bolts, lb, is measured parallel to the bolt axis from the surface of the masonry to the bolt head bearing surface. For bent-bar anchors, the effective embedment length is measured parallel to the bolt axis from the masonry surface to the bearing surface on the bent end minus one anchor bolt diameter.

Figure 2—Minimum Effective Embedment Lengths

Placement

Anchor bolts are required to be embedded in grout, with the exception that ¼ in. (6.4 mm) diameter anchors are permitted to be placed in mortar bed joints that are at least ½ in. (12.7 mm) thick. Excluding anchors placed in mortar bed joints, a minimum clearance of ¼ in. (6.4 mm) and ½ in. (12.7 mm) is required between the anchor bolt and the nearest surface of masonry for fine grout and coarse grout, respectively. This requirement applies to anchor bolts embedded in the top of a masonry element as well as those penetrating through the face shells of masonry as illustrated in Figure 2. While research (ref. 11) has shown that placing anchors in oversized holes in masonry unit face shells has no significant impact on the strength or performance of anchors compared to those placed in holes only slightly larger than the anchor diameter, the code has opted to maintain these clearance requirements as a convenient means of verifying that grout has adequately consolidated around the anchor bolt.
Although it rarely controls in typical masonry design, Building Code Requirements for Masonry Structures also requires that the distance between parallel anchors be at least equal to the diameter of the anchor, but not less than 1 in. (25.4 mm) to help ensure adequate anchor performance and grout consolidation around the anchor.

Existing masonry codes do not address tolerances for anchor bolt placement. In the absence of such criteria, construction tolerances used for placement of structural reinforcement could be modified for application to anchor bolts. In order to keep the anchor bolts properly aligned during grout placement, templates can be used to hold the bolts within the necessary tolerances. Templates, which are typically made of wood or steel, also prevent grout leakage in cases where anchors protrude from the side of a wall.

Projected Shear and Tension Areas

The projected tension breakout area, Apt, and the projected shear breakout area, Apv, for headed and bent-bar anchors are determined by Equations 1 and 2 as follows:

The anchor bolt edge distance, lbe, is measured in the direction of the applied load from the center of the anchor bolt to the edge of the masonry. When the projected areas of adjacent anchor bolts overlap, the portion of the overlapping area is reduced by one-half for calculating Apt or Apv as shown in Figure 3. Any portion of the projected area that falls within an open cell, open core, open head joint, or falls outside of the masonry element is deducted from the calculated value of Apt and Apv. A graphical representation of a tension breakout cone is shown in Figure 4.

Figure 3—Reduction of Projected Area When Failure Cones Overlap
Figure 4—Assumed Anchor Bolt Failure Cone

ALLOWABLE STRESS DESIGN OF ANCHOR BOLTS

Tension

The allowable axial tensile load, Ba, for headed and bent-bar anchor bolts is taken as the smaller of Equation 3, allowable axial tensile load governed by masonry breakout, and Equation 4, allowable axial tensile load governed by anchor yielding. For bent-bar anchors, the allowable axial tensile load must also be less than that determined by Equation 5 for anchor pullout.

Shear

The allowable shear load, Bv, for headed and bent-bar anchor bolts is taken as the smallest of Equation 6, allowable shear load governed by masonry breakout, Equation 7, allowable shear load as governed by crushing of the masonry, Equation 8, allowable shear load as governed by masonry pryout, and Equation 9, allowable shear load as governed by anchor yielding.

Combined Shear and Tension

Anchor bolts subjected to combined axial tension and shear must also satisfy the following unity equation:

The relationship between applied tension and shear loads versus allowable tension and shear loads is illustrated in Figure 5.

Figure 5—Unity Equation for Anchors Subjected to Combined Shear and Tension

STRENGTH DESIGN OF ANCHOR BOLTS

The design provisions for anchor bolts using the strength design method is nearly identical to that used for allowable stress design, with appropriate revisions to convert the requirements to produce nominal axial tension and shear design strengths. The strength reduction factors, Φ, for use in Equations 11 through 18 are taken equal to the following values:

  • when the nominal anchor strength is controlled by masonry breakout, masonry crushing, or anchor pryout, Φ is taken equal to 0.50,
  • when the nominal anchor strength is controlled by anchor bolt yielding, Φ is taken equal to 0.90,
  • when the nominal amchor strength is controlled by anchor pullout, Φ is taken equal to 0.65.

Tension

The nominal axial tensile strength, Ban, for headed and bent-bar anchor bolts is taken as the smaller of Equation 11, nominal axial tensile strength governed by masonry breakout, and Equation 12, nominal axial tensile strength governed by anchor yielding. For bent-bar anchors, the nominal axial tensile strength must also be less than that determined by Equation 13 for anchor pullout.

Shear

The nominal shear strength, Bvn, for headed and bent-bar anchor bolts is taken as the smallest of Equation 14, nominal shear strength governed by masonry breakout, Equation 15, nominal shear strength as governed by crushing of the masonry, Equation 16, nominal shear strength as governed by masonry pryout, and Equation 17, nominal shear strength as governed by anchor yielding.

Combined Shear and Tension

As with allowable stress design, anchor bolts subjected to combined axial tension and shear must also satisfy the following unity equation:

DESIGN EXAMPLE

Two ½ in (12.7 mm) headed anchors comprise a bolted connection for a roof beam to the side of an 8 in. (203mm) masonry wall, see Figure 5 below. The wall has a minimum specified compressive strength, f’m of 2,000 psi (13.8 MPa). The bolts have an effective yield stress of 60 ksi (413.7 MPa) with and effective embedment length and spacing between bolts of 6 in. (50.8 mm).

Allowable Stress Design

It can be assumed that the D + LR is the governing load combination. With this, the total design shear force for the connection is 1,600 lb (7.12 kN), with each anchor bolt resisting half of the total load. As is typical with bolted connections subjected to shear, the load is imparted at an offset distance, e which is equivalent to the additive thickness of the ledger and connector elements. This eccentric load generates a force couple with tensile forces in the anchor and bearing of the masonry wall. Using engineering judgment, the moment arm can be approximated as ⅚ times the distance from the center line of the bolt to the edge of the ledger, denoted as x for this example. The induced tension force on the entire connection can be calculated as follows:

Using Equation 1, one can determine the area of tensile breakout for each bolt to be 113.10 in² (729.68 cm²), however due to the proximity of the bolts to one another, there is an overlap in projected breakout area. To account for this, one must reduce the projected breakout area by one half of the overlap area when analyzing an individual bolt. The modified projected area for each bolt becomes:

Using the above equation, the modified Apt is found to be 90.99 in² (578.03 cm²).

In turn, the axial tensile strength is controlled by either masonry breakout (Equation 3) or anchor yielding (Equation 4) and determined as follows (Equation 5 is explicitly for bent-bar anchors and need not be checked):

For this example, the axial tensile strength is controlled by the masonry breakout strength, Bab.

Similarly, to determine the allowable shear strength, one would typically calculate the shear breakout area for each anchor. For this particular example, given the direction of shear loading and large edge distance, masonry shear breakout will not be the governing failure mode. Calculated strengths for masonry crushing (Equation 7), anchor pryout (Equation 8), and anchor yielding (Equation 9) are as follows:

In this instance, shear strength of each anchor is controlled by the masonry crushing strength, Bvc.

Checking the combined loading effects for an individual anchor against Equation 10 yields the following:

Because the demand to capacity ratio is less than 1.0, the design is satisfied.

Strength Design

It is assumed that the governing load combination for the connection is 1.2D+1.6LR. With that, the effects of the eccentric shear load are analyzed similarly to the allowable stress design example yielding a factored tensile force of 2,688 lb (11.96 kN) acting on the whole connection. The factored shear load acting on the connection is determined to be 2,240 lb (9.96 kN).

Again, citing Equation 1 and modifying it for the overlap of projected breakout area, Apt for each anchor bolt is found to be 90.99 in.² (578.03 cm²). Refer to the allowable stress design example for clarification.

Axial tensile strength determined by calculating masonry breakout (Equation 11) and anchor yielding (Equation 12) are as follows (as was the case before, Equation 13 need not be checked as this applies only to bent-bar anchors):

The nominal axial tensile strength is governed by the anchor yielding, Bans.

Nominal shear strength is controlled by masonry crushing (Equation 15), anchor pryout (Equation 16), and anchor yielding (Equation 17) and is checked as follows (as explained previously, for this example the wall geometry and direction of loading indicate shear breakout to be an unlikely failure mode):

For this example, the nominal shear strength for each anchor is controlled by masonry crushing, Bvnc.

Applying the appropriate strength reduction factors of Φ = 0.9 for anchor yielding under tensile loads and Φ = 0.5 for masonry crushing under shear loads, and checking the combined loading effects for an individual anchor against Equation 18 yields the following:

With the demand to capacity ratio less than 1.0, the design is satisfied.

ADDITIONAL RESOURCES

A supplemental anchor design spreadsheet (CMU-XLS-002-19, Ref. 12) is available for the design of both face and top mounted masonry anchors in accordance with the 2013 edition of Building Code Requirements for Masonry Structures.

NOTATIONS

Ab          = cross-sectional area of anchor bolt, in.² (mm²)
Apt         = projected area on the masonry surface of a right circular cone for calculating tensile breakout capacity of anchor bolts, in.² (mm²)
Apv        = projected area on the masonry surface of one-half of a right circular cone for calculating shear breakout capacity of anchor bolts, in.² (mm²)
Ba         = allowable axial force on anchor bolt, lb (N)
Bab       = allowable axial tensile load on anchor bolt when governed by masonry breakout, lb (N)
Ban       = nominal axial strength of anchor bolt, lb (N)
Banb     = nominal axial tensile strength of anchor bolt when governed by masonry breakout, lb (N)
Banp     = nominal axial tensile strength of anchor bolt when governed by anchor pullout, lb (N)
Bans      = nominal axial tensile strength of anchor bolt when governed by steel yielding, lb (N)
Bap       = allowable axial tensile load on anchor bolt when governed by anchor pullout, lb (N)
Bas       = allowable axial tensile load on anchor bolt when governed by steel yielding, lb (N)
Bv         = allowable shear force on anchor bolt, lb (N)
Bvb       = allowable shear load on an anchor bolt when governed by masonry breakout, lb (N)
Bvc       = allowable shear load on anchor bolt when governed by masonry crushing, lb (N)
Bvn       = nominal shear strength of anchor bolt, lb (N)
Bvnb     = nominal shear strength of anchor bolt when governed by masonry breakout, lb (N)
Bvnc     = nominal shear strength of anchor bolt when governed by masonry crushing, lb (N)
Bvnpry  = nominal shear strength of anchor bolt when governed by anchor pryout, lb (N)
Bvns     = nominal shear strength of anchor bolt when governed by steel yielding, lb (N)
Bvpry   = allowable shear load on an anchor bolt when governed by anchor pryout, lb (N)
Bvs       = allowable shear load on an anchor bolt when governed by steel yielding, lb (N)
ba        = unfactored axial force on anchor bolt, lb (N)
baf       = factored axial force in anchor bolt, lb (N)
bv        = unfactored shear force on anchor bolt, lb (N)
bvf       = factored shear force in anchor bolt, lb (N)
db        = nominal diameter of anchor bolt, in. (mm)
e          = eccentricity of applied loads on bolted connection, in. (mm)
eb        = projected leg extension of bent bar anchor, measured from inside edge of anchor at bend to farthest point of anchor in the plane of the hook, in. (mm)
f’m       = specified compressive strength of masonry, psi (MPa)
fy         = specified yield strength of steel for anchors, psi (MPa)
lb         = effective embedment length of anchor bolts, in. (mm)
lbe        = anchor bolt edge distance, measured in direction of load, from edge of masonry to center of the cross section of anchor bolt, in. (mm)
s          = spacing between anchors, in. (mm)
x          = depth from center line of anchor to edge of ledger
Φ         = strength reduction factor

REFERENCES

  1. Building Code Requirements for Masonry Structures, TMS 402-13/ACI 530-13/ASCE 5-13, Reported by the Masonry Standards Joint Committee, 2013.
  2. Specification for Masonry Structures, TMS 605-13/ACI 530.1-13/ASCE 6-13, Reported by the Masonry Standards Joint Committee, 2013.
  3. International Building Code, International Code Council, 2012.
  4. International Residential Code, International Code Council, 2012.
  5. Building Code Requirements for Masonry Structures, TMS 402-11/ACI 530-11/ASCE 5-11, Reported by the Masonry Standards Joint Committee, 2011.
  6. Standard Specification for Carbon Structural Steel, ASTM A36-12, ASTM International, 2012.
  7. Standard Specification for Carbon Steel Bolts and Studs, 60,000 psi Tensile Strength, ASTM A307-12, ASTM International, 2012.
  8. Standard Test Methods for Strength of Anchors in Concrete and Masonry Elements, ASTM E488-10, ASTM International, 2010.
  9. Allowable Stress Design of Concrete Masonry, TEK 14-07C, Concrete Masonry & Hardscapes Association, 2011.
  10. Strength Design Provisions for Concrete Masonry, TEK 14-04B, Concrete Masonry & Hardscapes Association, 2008.
  11. Testing of Anchor Bolts in Concrete Block Masonry, Tubbs, J. B., Pollock, D. G., and McLean, D. I., The Masonry Society Journal, 2000.

TEK 12-03C, Revised 2013. CMHA and the companies disseminating this technical information disclaim any and all responsibility and liability for the accuracy and the application of the information contained in this publication.