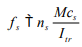Design of Concrete Masonry Noncomposite (Cavity) Walls
INTRODUCTION
When selecting a building enclosure, concrete masonry cavity walls are considered to be one of the best solutions available for all types of buildings. From both an initial cost and life-cycle cost perspective, cavity wall construction is highly regarded as the prime choice in many applications.
Cavity walls typically consist of an inner wythe of concrete masonry units that are tied to an exterior wythe of architectural masonry units. The cavity space between the wythes is normally 2 to 4 ½ in. (51 to 114 mm) wide, easily accommodating rigid board insulation. The two wythes together provide a wall that is highly resistant to wind driven rain, absorbs and reflects sound, provides good thermal performance, and has excellent fire resistance characteristics.
Masonry walls constructed of two or more wythes can technically be classified in one of three ways, depending on how the wythes are designed and detailed. These wall types include composite, noncomposite and veneer assemblies. In noncomposite construction, covered in this TEK, each wythe is connected to the adjacent wythe with metal wall ties, but they are designed such that each wythe individually resists the loads imposed on it. Composite walls are designed so that the wythes act together as a single element to resist structural loads. This requires the masonry wythes to be connected by masonry headers or by a mortar- or grout-filled collar joint and wall ties (see ref. 4). In a veneer wall, the backup wythe is designed as the loadbearing system while the veneer provides a nonloadbearing architectural wall finish that transfers loads to the backup wythe through wall ties (see refs. 5, 6). Although Building Code Requirements for Masonry Structures (ref. 1) defines a cavity wall as a noncomposite masonry wall, the term cavity wall is also commonly used to describe a veneer wall with masonry backup.
This TEK illustrates the design of noncomposite concrete masonry walls based on Building Code Requirements for Masonry Structures (ref. 1), referred to here as the MSJC code. Each wythe of a noncomposite wall system can be designed to accommodate all types of loads, including gravity loads from roofs, walls and floors, as well as lateral loads from wind or earthquakes. The MSJC code design provisions are used to size these masonry walls.
STRUCTURAL DESIGN
The MSJC code includes noncomposite design provisions for both allowable stress design (Chapter 2) and empirical design (Chapter 5). The assumptions and relevant governing equations for each of these design approaches is given in references 2 and 3 respectively.
Concrete masonry cavity walls can be designed as either reinforced or unreinforced walls. For unreinforced design, flexural tensile stresses in masonry are resisted by bond developed between the masonry units and mortar; axial tension is not permitted (ref. 1). If direct axial tension is encountered in a design, reinforcement must be used. In reinforced masonry design, all tension is assumed to be resisted by reinforcement.
Empirical Design
Empirical design can be an expedient approach for typical loadbearing structures subjected to nominal wind loads (basic wind speed ≤ 110 mph, (177 km/h) (MSJC 5.1.2.2) and located in areas of low seismic risk, as it cannot be used for the design of seismic force resisting systems in SDC (Seismic Design Category) B or higher (MSJC 5.1.2.1). Empirical design utilizes prescriptive provisions, outlining criteria such as wall height to thickness ratios, minimum wall thickness and maximum building height.
References 1 and 3 contain maximum length-to-thickness or height-to-thickness ratios for empirically designed walls. When using these ratios for noncomposite multiwythe walls, the total wall thickness is taken as the sum of the nominal thicknesses of each wythe, neglecting the presence of any cavity thickness. Compressive stress is based on the gross cross-sectional area of all wythes, including hollow cells but not including the cavity between the wythes. When floor or roof loads are carried on only one wythe, only the gross cross-sectional area of that wythe is used to check the axial capacity. In addition, these walls must meet the following requirements for wall ties connecting the wythes:
- wall ties of wire size W2.8 (3/16 in., MW 18), or metal wire of equivalent stiffness, spaced at a maximum of 24 in. (610 mm) o.c. vertically and 36 in. (914 mm) o.c. horizontally, with at least one wall tie for each 4½ ft² (0.42 m²) of wall area,
- walls constructed with hollow units must use rectangular ties,
- walls constructed with solid units must use Z-shaped ties with hooks at least 2 in. (51 mm) long,
- wall ties may not have drips,
- additional ties are required within 12 in. (305 mm) of all openings and must be spaced no more than 3 ft (914 mm) apart around the perimeter of the opening.
Requirements for bonding with joint reinforcement are the same as those for wall ties with the following exceptions: cross wire size may not be smaller than W1.7 (9 gage, MW 11) and the supported wall area per cross wire may not exceed 2⅔ ft² (0.25 m²). In addition, the longitudinal wires must be embedded in mortar.
Allowable Stress Design
Similar to empirical design, MSJC allowable stress design includes prescriptive requirements for bonding wythes of noncomposite walls via wall ties, adjustable ties and joint reinforcement.
For rectangular ties, Z ties (for use with other than hollow units) and ladder or tab-type joint reinforcement, ties or cross wires of joint reinforcement, ties must be placed with a maximum spacing of 36 in. (914 mm) horizontally and 24 in. (610 mm) vertically. The minimum number of ties is one per:
- 2⅔ ft² (0.25 m²) of wall for wire size W 1.7 (9 gage, MW 11), and
- 4½ ft² (0.42 m²) of wall for wire size W 2.8 (3/16 in., MW 18).
For adjustable ties, one tie must be provided for each 1.77 ft² (0.16 m²) of wall; maximum horizontal and vertical spacing is 16 in. (406 mm); misalignment of bed joints from one wythe to the other may not exceed 1 ¼ in. (31.8 mm); the maximum clearance between connecting parts of the tie is 1/16 in. (1.6 mm); and pintle ties must have at least two pintle legs of wire size W2.8 (3/16 in., MW 18) (see also Figure 1).
For noncomposite masonry walls, the following additional requirements apply.
- Collar joints are not to contain headers, or be filled with mortar or grout.
- Gravity loads from supported horizontal members are to be resisted by the wythe nearest the center of the span.
- Bending moments about the weak axis of the wall and transverse loads are distributed to each wythe according to relative stiffness. This can be determined by:
Wi = WT [EmIi/(EmIi+ EmI0)]
Wo = WT [EmI0/(EmIi+ EmI0)] - Loads acting parallel to the wall are resisted by the wythe to which they are applied.
- The cavity width between the wythes is limited to 4½ in. (114 mm) unless a detailed wall tie analysis is performed.
DESIGN EXAMPLES
The following examples illustrate the use of noncomposite masonry employing empirical and allowable stress design methods. Although there are no specific provisions in MSJC for noncomposite wall design using strength design, strength design could be used provided the same load distribution principles as presented for allowable stress design are employed.
Empirical Design Design Example:
Design the top story of a two-story noncomposite double wythe masonry wall system supported on continuous footings. Note that the design of the lower story, though not shown, is performed in the same manner, except that the floor live and dead loads from the upper story are also accounted for.
Given:
| unsupported wall height | = 10 ft (3.01 m) |
| superimposed gravity dead load | = 220 plf (3.2 kN/m) |
| superimposed gravity live load | = 460 plf (6.7 kN/m) |
| net superimposed uplift from wind | = 120 plf (1.8 kN/m) |
| wind pressure | = 24 psf (1,149 Pa) |
| eccentricity of all gravity loads | = 0 |
| f’m | = 1,500 psi (10.3 MPa) |
| Em | = 1,350 ksi (9,308 MPa) |
Wall lateral support requirement: l/t or h/t < 18, so minimum required wall thickness = h/18
= 10 ft (12 in./ft)/18
= 6.7 in. (169 mm)
Try a 4-in. (102 mm) outer wythe and 6-in. (152 mm) inner wythe (providing a total nominal wall thickness of 10 in. (254 mm)), and check allowable axial compressive stress due to dead and live loads (gravity loads are carried by the inner wythe only):
| dead: | roof | 220 lb/ft |
| wythe = 10 ft x 26 psf (ref. 8) | 260 lb/ft | |
| live: | roof | 460 lb/ft |
| total load: | 940 lb/ft (13.7 kN/m) |
Gross area of 6-in. (152-mm) wythe = 67.5 in.²/ft (ref. 7)
fa = 940 lb/ft/(67.5 in.²/ft) = 13.9 psi (0.096 MPa)
Fa = 75 psi (0.52 MPa) for Type M or S mortar, 70 psi (0.48 MPa) for Type N mortar (ref. 1)
fa < Fa (OK for all mortar types)
Per MSJC code section 5.8.3.1, the net uplift on the roof must be resisted by an anchorage system. Use a bond beam at the top of the inner wythe with vertical reinforcement to the foundation to provide this resistance.
ASD Reinforced Design Example:
Given:
| unsupported wall height | = 18 ft (5.5 m) |
| wind load, w | = 36 psf (1,724 Pa) |
| net roof uplift at top of wall | = 400 plf (5.8 kN/m) ) |
| eccentricity of all vertical loads | = 0 |
| f’m | = 1,500 psi (0.0718 MPa ) |
| unit density | = 115 pcf (1,842 kg/m³) |
| Grade 60 reinforcement |
Note: The 36 psf (1,724 Pa) wind load is much higher than is generally applicable when using empirical design.
Design the inside wythe first, as it must resist the uplift in addition to the flexural loads. Try two 6-in. (152 mm) wythes with No. 5 (M #16) reinforcement at 32 in. (813 mm) o.c.
Determine reinforcement needed for uplift at midheight:
uplift = 400 lb/ft – 34 lb/ft² (18 ft/2) = 94 lb/ft (1.37 kN/m) (ref. 8)
reinforcement needed = [(94 lb/ft)(32 in.)/(12 in./ft)]/[1.333(24,000 psi)] = 0.0078 in.²
As available for flexure = 0.31 – 0.0078 = 0.3022 in.²
Ms = FsAsjd = 1.333 (24,000 psi) (0.3022 in.²)(0.894)(2.813 in.)
= 24,313 lb-in. for 32 in. width
= 9,117 lb-in./ft (3,378 N⋅m/m) > 8,996 lb-in./ft (3,333 N⋅m/m), therefore Mm controls
Determine applied moment:
Since the wythes are identical, each would carry ½ the lateral load or ½ (36 psf) = 18 psf (124 kPa)
Mmax = wl²/8 = (18 psf)(18 ft)²(12 in./ft)/8
= 8,748 lb-in./ft (3,241 N⋅m/m) < 8,996 lb-in./ft (3,333 N⋅m/m) OK
Check shear:
Vmax = wl/2 = (18psf)(18 ft)/2 = 162 lb/ft (2.36 kN/m)
fv = Vmax/bd = 162 lb/ft/(12 in.)(2.813 in.) = 4.80 psi (33 kPa)
Fv = 37 x 1.333 = 51 psi (351 kPa)
4.80 psi (33 kPa) < 51 psi (351 kPa) OK
A quick check of the outside wythe shows that the same reinforcement schedule will work for it as well. Therefore, use two 6-in. (152-mm) wythes with No. 5 (M #16) vertical reinforcement at 32 in. (813 mm) o.c.
This wall could be designed using an unreinforced 4-in. (102 mm) outside wythe and a reinforced 8-in. (203-mm) inside wythe, with lateral loads distributed to each wythe according to the uncracked stiffness per MSJC section 1.9.2. Experience has shown, however, that the design would be severely limited by the capacity of the unreinforced outside wythe. Additionally, such a design could be used only in SDC A or B since 4-in. (102 mm) concrete masonry does not have cores large enough to reinforce.
Another alternative would be to design this system treating the 4 in. (102 mm) outer wythe as a nonloadbearing veneer. Designing this wall as a 4-in. (102 mm) veneer with an 8-in. (203 mm) reinforced structural backup wythe would result in No. 5 bars at 16 in. (M #16 at 406 mm) on center. This is the same amount of reinforcement used in the example above (two 6-in. (152 mm) wythes with No. 5 (M #16) at 32 in. (813 mm) on center). However, because the 6-in. (152 mm) units have smaller cores, 30% less grout is required.
The design using two 6-in. (152-mm) reinforced wythes has the following advantages over veneer with structural backup:
- no limitation on SDC as when a veneer or an unreinforced outer wythe is used,
- no limitation on wind speed as with a veneer,
- equal mass on both sides of the wall permitting the use of the prescriptive energy tables for integral insulation, and
- the flexibility of using units with different architectural finishes on each side.
NOMENCLATURE
As = effective cross-sectional area of reinforcement, in.²(mm²)
b = width of section, in. (mm)
d = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
Em = modulus of elasticity of masonry, psi (MPa)
Es = modulus of elasticity of steel, psi (MPa)
Fa = allowable compressive stress due to axial load only, psi (kPa)
Fb = allowable compressive stress due to flexure only, psi (kPa)
Fs = allowable tensile or compressive stress in reinforcement, psi (kPa)
Fv = allowable shear stress in masonry, psi (MPa)
fa = calculated compressive stress in masonry due to axial load only, psi (kPa)
f’m = specified compressive strength of masonry, psi (kPa)
h = effective height, in. (mm)
fv = calculated shear stress in masonry, psi (MPa)
Ii = average moment of inertia of inner wythe, in.4/ft (m4/m)
Io = average moment of inertia of outer wythe, in.4/ft (m4/m)
j = ratio of distance between centroid of flexural compressive forces and centroid of tensile forces to depth d
k = ratio of distance between compression face of wall and neutral axis to depth d
l = clear span between supports, in. (mm)
M = moment at the section under consideration, in.-lb/ft (N⋅m/m)
Mm = flexural capacity (resisting moment) when masonry controls, in.-lb/ft (N⋅m/m)
Mmax = maximum moment at the section under consideration, in.-lb/ft (N⋅m/m)
Ms = flexural capacity (resisting moment) when reinforcement controls, in.-lb/ft (N⋅m/m)
t = nominal thickness of a member, in. (mm)
Vmax = maximum shear at the section under consideration, lb/ft (kN/m)
Wi = percentage of transverse load on inner wythe
Wo = percentage of transverse load on outer wythe
WT = total transverse load
w = wind pressure, psf (Pa)
ρ = reinforcement ratio
REFERENCES
- Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
- ASD of Concrete Masonry (2012 IBC & 2011 MSJC), TEK 14-07C, Concrete Masonry & Hardscapes Association, 2004.
- Empirical Design of Concrete Masonry Walls, TEK 1408B, Concrete Masonry & Hardscapes Association, 2003
- Structural Design of Unreinforced Composite Masonry, TEK 16-02B, Concrete Masonry & Hardscapes Association, 2001.
- Concrete Masonry Veneers, TEK 03-06C, Concrete Masonry & Hardscapes Association, 2012.
- Reinforced Composite Concrete Masonry Walls, TEK 1603B, Concrete Masonry & Hardscapes Association, 2006.
- Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.