Home / Technical Resources / openings in walls

Resources

ASD of Concrete Masonry Lintels Based on the 2012 IBC/2011 MSJC

August 2018

INTRODUCTION

Lintels and beams are horizontal structural members designed to carry loads above openings. Although lintels may be constructed of grouted and reinforced concrete masonry units, precast or cast-in-place concrete, or structural steel, this TEK addresses reinforced concrete masonry lintels only. Concrete masonry lintels have the advantages of easily maintaining the bond pattern, color, and surface texture of the surrounding masonry and being placed without need for special lifting equipment.

Concrete masonry lintels are sometimes constructed as a portion of a continuous bond beam. This construction provides several benefits: it is considered to be more advantageous in high seismic areas or areas where high winds may be expected to occur; control of wall movement due to shrinkage or temperature differentials is more easily accomplished; and lintel deflection may be substantially reduced.

The content presented in this TEK is based on the requirements of the 2012 IBC (ref. 1a), which in turn references the 2011 edition of the MSJC Code (ref. 2a).

Significant changes were made to the allowable stress design (ASD) method between the 2009 and 2012 editions of the IBC. These are described in detail in TEK 14-07C, ASD of Concrete Masonry (2012 IBC & 2011 MSJC) (ref. 3), along with a detailed presentation of all of the allowable stress design provisions of the 2012 IBC.

DESIGN LOADS

Vertical loads carried by lintels typically include:

distributed loads from the dead weight of the lintel, the dead weight of the masonry above, and any floor and roof loads, dead and live loads supported by the masonry; and
concentrated loads from floor beams, roof joists, or other beams framing into the wall. Axial load carried by lintels is negligible.

Most of these loads can be separated into the four types illustrated in Figure 1: uniform load acting over the effective span; triangular load with apex at mid-span acting over the effective span; concentrated load; and uniform load acting over a portion of the effective span.

The designer calculates the effects of each individual load and then combines them using superposition to determine the overall effect, typically by assuming the lintel is a simply supported beam.

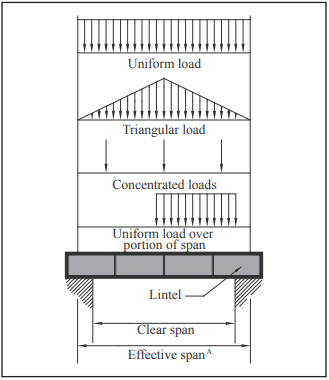
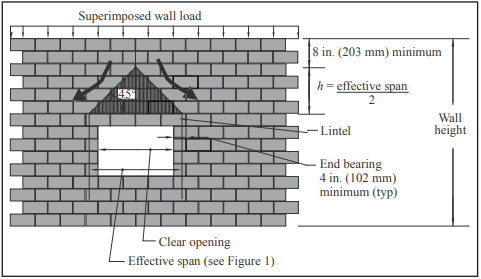
^A Effective span length is the center-to-center distance between supports.

Arching Action

For some configurations, the masonry will distribute applied loads in such a manner that they do not act on the lintel. This is called arching action of masonry. Arching action can be assumed when the following conditions are met (see also Figure 2):

masonry wall laid in running bond,
sufficient wall height above the lintel to permit formation of a symmetrical triangle with base angles of 45° from the horizontal as shown in Figure 2,
at least 8 in. (203 mm) of wall height above the apex of the 45° triangle,
minimum end bearing (4 in. (102 mm) typ.) is maintained,
control joints are not located adjacent to the lintel, and
sufficient masonry on each side of the opening to resist lateral thrust from the arching action.

Lintel Loading

The loads supported by a lintel depend on whether or not arching action can occur. When arching is not present, the lintel self-weight, the full weight of the wall section above the lintel and superimposed loads are considered. Self weight is a uniform load based on lintel weight (see Table 1).

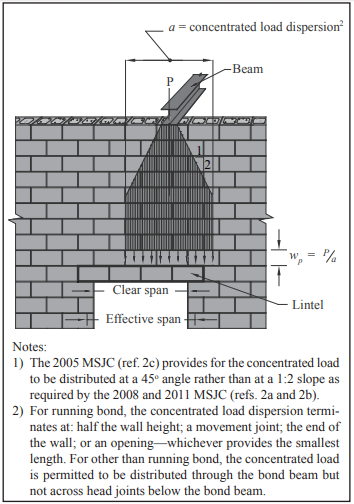
When arching occurs, the wall weight supported by the lintel is taken as the wall weight within the triangular area below the apex (see Figure 2 and Table 2). This triangular load has a base equal to the effective span length of the lintel and a height of half the effective span. Any superimposed roof and floor live and dead loads outside this triangle are neglected, since they are assumed to be distributed to the masonry on either side of the lintel. Loads applied within the triangle need to be considered, however.

Concentrated loads are assumed to be distributed as illustrated in Figure 3. The load is then resolved onto the lintel as a uniform load, with a magnitude determined by dividing the concentrated load by this length. In most cases, this results in a uniform load acting over a portion of the lintel span.

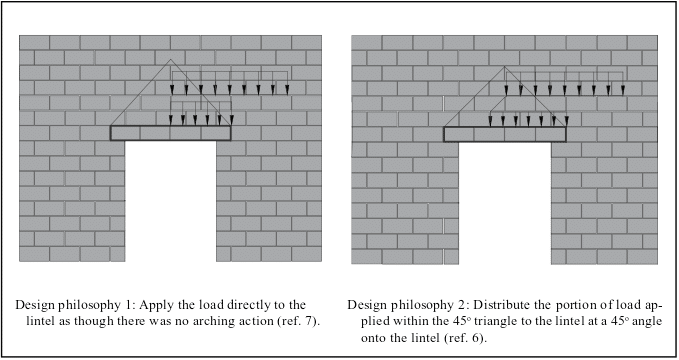
The MSJC (ref. 2) does not address how to apply uniform loads that are applied within the 45° triangle. There are two schools of thought (see Figure 4):

Apply the full uniform load directly to the lintel without further distribution just as though there was no arching for those loads.
Distribute the portions of uniform loads that are applied within the 45o triangle to the lintel. These uniform loads within the 45o triangle may be dispersed and distributed at a 45o angle onto the lintel (ref. 5).

Lintels are required to be designed to have adequate stiffness to limit deflections that would adversely affect strength or serviceability. In addition, the deflection of lintels supporting unreinforced masonry is limited to the clear lintel span divided by 600 to limit damage to the supported masonry (ref. 2).

Table 1—Lintel Weights per Foot, D(lintel), lb/ft (kN/m) (A)

^A Face shell mortar bedding. Unit weights: grout = 140 pcf (2,242 kg/m³); lightweight masonry units = 100 pcf (1602 kg/m³); normal weight units = 135 pcf (2,162 kg/m³).

Figure 3—Distribution of Concentrated Load for Running Bond Construction

Figure 4—Methods of Applying Uniform Loads that Occur Within the 45° Triangle

DESIGN TABLES

Tables 3 and 4 present allowable shear and moment, respectively, for various concrete masonry lintels, with various amounts of reinforcement and bottom cover based on a specified compressive strength of masonry, f’m = 1,500 psi (10.3 MPa) and the allowable stress design provisions of the 2011 MSJC (ref. 2a) and the 2012 IBC (ref.1a).

Table 3—Allowable Shear Capacities for Concrete Masonry LintelsA

DESIGN EXAMPLE

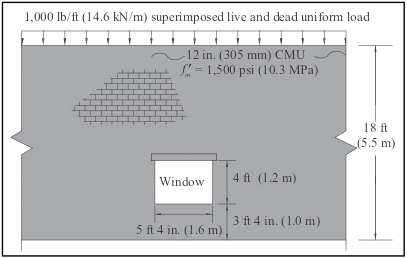
Design a lintel for a 12 in. (305 mm) normal weight concrete masonry wall laid in running bond with vertical reinforcement at 48 in. (1.2 m) o.c. The wall configuration is shown in Figure 5.

Case 1—Arching Action

Check for Arching Action. Determine the height of masonry required for arching action. Assuming the lintel has at least 4 in. (102 mm) bearing on each end, the effective span is:

L = 5.33 + 0.33 = 5.67 ft (1.7 m).

The height of masonry above the lintel necessary for arching to occur in the wall (from Figure 2) is h + 8 in. (203 mm) = L/2 + 8 in. = 3.5 ft (1.1 m).
Based on an 8-in. (203-mm) high lintel, there is 18.0 – (3.33 + 4.0 + 0.67) = 10.0 ft (3.0 m) of masonry above the lintel. Therefore, arching is assumed and the superimposed uniform load is neglected.

Design Loads. Because arching occurs, only the lintel and wall dead weights are considered. Lintel weight, from Table 1, for 12 in. (305 mm) normal weight concrete masonry units assuming an 8 in. (203 mm) height is D_lintel = 88 lb/ft (1.3 kN/m).

For wall weight, only the triangular portion with a height of 3.5 ft (1.1 m) is considered. From Table 2, wall dead load is:

D_wall = 63 lb/ft² (3.5 ft)
= 221 lb/ft (3.2 kN/m) at the apex.

Maximum moment and shear are determined using simply supported beam relationships. The lintel dead weight is considered a uniform load, so the moment and shear are,

M_lintel = D_lintelL²/8
= (88)(5.7)²/8
= 357 lb-ft (0.48 kN-m)
V_lintel = D_lintelL/2
= (88)(5.7)/2 = 251 lb (1.1 kN)

For triangular wall load, moment and shear are,

M_wall = D_wallL²/12
= (221)(5.7)²/12
= 598 lb-ft (0.81 kN-m)
V_wall = D_wallL/4
= (221)(5.7)/4 = 315 lb (1.4 kN)

Because the maximum moments for the two loading conditions occur in the same locations on the lintel (as well as the maximum shears), the moments and shears are superimposed and summed:

M_max = 357 + 598
= 955 lb-ft = 11,460 lb-in (1.3 kN-m)
V_max = 251 + 315
= 566 lb (2.5 kN)

Lintel Design. From Tables 3 and 4, a 12 x 8 lintel with one No. 4 (M#13) bar and 3 in. (76 mm) or less bottom cover has adequate strength (M_all = 22,356 lb-in. (2.53 kN-m) and V_all = 2,152 lb (9.57 kN)). In this example, shear was conservatively computed at the end of the lintel. However, Building Code Requirements for Masonry Structures (ref. 2) allows maximum shear to be calculated using a distance d/2 from the face of the support.

Case 2—No Arching Action

Using the same example, recalculate assuming a 2 ft (0.6 m) height from the bottom of the lintel to the top of the wall. For ease of construction, the entire 2 ft (0.6 m) would be grouted solid, producing a 24 in. (610 mm) deep lintel.

Because the height of masonry above the lintel is less than 3.5 ft (1.1 m), arching cannot be assumed, and the superimposed load must be accounted for.

D_lintel = 264 lb/ft (3.9 kN/m), from Table 1. Because the lintel is 24 in. (610 mm) deep, there is no additional dead load due to masonry above the lintel.

W_total = 264 lb/ft + 1,000 lb/ft
= 1,264 lb/ft (18.4 kN/m)

M_max = wL²/8
= (1,264)(5.7)²/8 x 12 in./ft
= 61,601 lb-in (7.0 kN-m)

V_max = wL/2 = (1,264)(5.7)/2
= 3,602 lb (16.0 kN)

From Tables 3 and 4, a 12 x 24 lintel with one No. 4 (M#13) reinforcing bar and 3 in. (76 mm) or less bottom cover is adequate (M_all = 122,872 lb-in. (13.88 kN-m) and V_all = 10,256 lb (45.62 kN).

Figure 5—Wall Configuration for Design Example

NOTATIONS

b = width of lintel, in. (mm)
D_lintel = lintel dead load, lb/ft (kN/m)
D_wall = wall dead load, lb/ft (kN/m)
d = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
f’_m = specified compressive strength of masonry, psi (MPa)
h = half of the effective lintel span, L/2, ft (m)
L = effective lintel span, ft (m)
M_all = allowable moment, in.-lb (N⋅m)
M_lintel = maximum moment due to lintel dead load, in.-lb (N⋅m)
M_max = maximum moment, in.-lb (N⋅m)
M_wall = maximum moment due to wall dead load moment, in.-lb (N⋅m)
V_all = allowable shear, lb (N)
V_lintel = maximum shear due to lintel dead load, lb (N)
V_max = maximum shear, lb (N)
V_wall = maximum shear due to wall dead load, lb (N)
W_total = total uniform live and dead load, lb/ft (kN/m)
w = uniformly distributed load, lb/in. (N/mm)

REFERENCES

International Building Code. International Code Council.
1. 2012 Edition
Building Code Requirements for Masonry Structures. Reported by the Masonry Standards Joint Committee. a. 2011 Edition: TMS 402-11/ACI 530-11/ASCE 5-11
ASD of Concrete Masonry (2012 IBC & 2011 MSJC), TEK 14-07C, Concrete Masonry & Hardscapes Association, 2011.
Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.
Openings in Concrete Masonry Walls (Part 1), Masonry Chronicles Winter 2008-09, Concrete Masonry Association of California and Nevada, 2009.

Noise Control With Concrete Masonry

August 2018

INTRODUCTION

Sound control is an important design consideration in most buildings. Sound control involves two important properties: sound transmission and sound absorption, as depicted in Figure 1. The International Building Code (IBC, refs. 1, 2) contains minimum requirements for sound transmission in certain situations (see Sound Transmission Class Ratings of Concrete Masonry Walls, TEK 13-01D, ref. 3). However, the IBC does not contain minimum requirements for sound absorption, although proper control of sound reﬂected back into the room is a very important design function in many buildings as well, such as concert halls, gymnasiums, places of assembly, rooms containing loud equipment.

Concrete masonry is an ideal noise control material for both properties: it can act as a barrier by diffusing incident noise over a wide range of frequencies; and it can be an effective sound absorption material for absorbing noise generated within a room. This TEK discusses the sound absorption and sound transmission properties of concrete masonry, and provides general design guidance to help provide a good acoustic environment.

Figure 1—Sound Attenuation Characteristics of Concrete Masonry

MAXIMIZING SOUND ABSORPTION

Sound absorption control involves minimizing sound reﬂection, so that the noise generated within the space is not echoed back into the space. Sound absorption is most important in applications like assembly areas or concert halls. The extent of control provided by a particular surface depends on that surface’s ability to absorb rather than reﬂect sound waves. This ability is estimated by the surface’s sound absorption coefﬁcient: an indication of its sound absorbing efﬁciency. A surface which can theoretically absorb 100% of incident sound would have a sound absorption coefﬁcient of 1. Similarly, a surface capable of absorbing 45% of incident sound has a sound absorption coefﬁcient of 0.45.

Because the sound absorption coefﬁcient typically varies with the frequency of the incident sound, the sound absorption coefﬁcients measured at various frequencies are averaged together to produce an overall absorption coefﬁcient. Standard Test Method for Sound Absorption and Sound Absorption Coefﬁcients by the Reverberation Room Method, ASTM C423 (ref. 4) prescribes the test method and calculations. Traditionally, sound absorption has been reported in terms of the noise reduction coefﬁcient (NRC), determined by taking a mathematical average of the sound absorption coefﬁcients obtained at frequencies of 250, 500, 1,000 and 2,000 Hertz. More recently, the Sound Absorption Average (SAA) has been added to ASTM C423. Although the SAA is very similar to NRC, it is determined by averaging the sound absorption coefﬁcients obtained at the twelve one-third octave bands from 200 through 2,500 Hz. ASTM C423 requires that both NRC and SAA be reported. Experience in the concrete masonry industry has shown that the new SAA values and the old NRC values vary little and generally are within 1 or 2 percentage points of each other.

Sound absorption values depend primarily on the surface texture and porosity of the material under consideration. More porous and open-textured surfaces are able to absorb more sound and, hence, have a higher value. This is reﬂected in the concrete masonry NRC values listed in Table 1. Note that painting a concrete masonry wall closes small surface openings, and hence decreases the wall’s sound absorption value.

Table 1—Approximate Noise Reduction Coefﬁcients

MINIMIZING SOUND TRANSMISSION

Sound insulation, as between dwelling units, is accomplished by designing walls to minimize sound transmission. For this purpose, effectiveness primarily depends on wall weight, rather than on surface texture. In general, the heavier a concrete masonry wall is, the more effectively it will block sound transmission.

The sound transmission class (STC) rating provides an indication of how effectively a given wall prevents sound transmission across a range of frequencies. STC ratings for concrete masonry walls are determined using Standard Method for Determining the Sound Transmission Class Rating for Masonry Walls, TMS 0302 (ref. 5). TEK 13-01D, Sound Transmission Class Ratings of Concrete Masonry Walls, contains a complete discussion on determining STC ratings, applicable building code requirements, as well as tabulated values for various concrete masonry walls.

WALL SELECTION

When used for noise control, concrete masonry walls should be evaluated for both surface texture and density. Sound transmission is reduced by using heavier walls, but may be increased by using units with a very open surface texture. Transmission loss characteristics of unpainted, open-textured units can be increased by plastering or painting, although this will also result in a corresponding reduction in the sound absorption (SAA or NRC) of the block.

In some cases, the designer may wish to use both the transmission loss and absorption properties of concrete masonry to advantage. For example, using open textured units in a cavity wall with back plastering on the inside face of one or both wythes provides sound absorption on both sides of the wall as well as sound transmission reduction. Another option for providing both effective sound absorption and sound transmission loss is the use of acoustical concrete masonry units, such as those shown in Figure 2. These units typically have an opening molded into the face shell, to allow sound energy to readily enter the masonry cells. The cells are designed to incorporate systems such as metal septa and/or ﬁbrous ﬁllers to dissipate the sound energy and minimize sound transmission.

Figure 2—Examples of Acoustical Concrete Masonry Units (viewed from bottom)

DESIGN AND CONSTRUCTION

Early in the design, a detailed noise survey should be conducted to determine the outside noise level and the anticipated background noise level in the various building areas. A building layout can then be developed which will help reduce noise transmission from one area to another. Effective sound control depends on proper layout and wall selection as well as good construction techniques.

Sound will be easily transmitted through any opening in a wall. An improperly ﬁtted corridor door is a prime source of sound leakage, as well as openings around ducts, piping and electrical outlets which are improperly ﬁtted or sealed. A crack just 0.007 in. (0.178 mm) wide along the top of a 12½ ft (3.8 m) wall will allow as much transmitted sound as a 1 in.² (645 mm²) hole. Hence, it is very important to seal all cracks, joints and gaps to maintain the acoustical integrity of the wall.

Building design and layout can also impact the building’s acoustic effectiveness. Planning early in the design process can help alleviate potential problem areas farther down the line. For example, individual spaces should be planned to minimize common walls whenever possible (see Figure 3), and to place adjacent spaced such that quieter areas (such as bedrooms) abut each other, and noisy areas (such as kitchens) abut similar noisy areas (see Figure 4).

When considering building layout, also note that sound travels most effectively in straight lines. Every time sound energy changes direction, some of it is absorbed and some diffused, hence reducing the amount that is transmitted. For example, Figure 5 shows that simply offsetting hallway doors can decrease the sound transmitted from one space to another through the doors. Separating windows will have a similar effect (see Figure 6).

Any wall penetration will potentially transmit sound. Therefore, plan to eliminate penetration whenever possible (see Figure 7). When unavoidable, partial wall penetrations such as electrical boxes should be completely sealed with joint sealant. Through-wall openings should be completely sealed, after ﬁrst ﬁlling gaps with foam, cellulose ﬁber, glass ﬁber, ceramic ﬁber or mineral wool. See Sound Transmission Class Ratings of Concrete Masonry Walls, TEK 13-01D, for a more complete discussion of minimizing sound transmission through wall penetrations.

Finally, building heating and cooling ducts offer a potential noise pathway throughout a building. There are many ways to absorb or dissipate this noise, including acoustic linings and splitters to help break up and disperse the sound energy (see Figure 8). Any changes to the building’s ductwork will also potentially impact heating and cooling distribution. These effects should be considered during the HVAC system design.

Figure 3—Plan the Building Layout to Minimize Common Walls

Figure 5—Offset Doors Opening onto the Same Hallway

Figure 6—Move Windows Farther Away from Common Wall

Figure 8—Acoustic Controls for Heating and Cooling Ducts

REFERENCES

2003 International Building Code. International Code Council, 2003.
2006 International Building Code. International Code Council, 2006.
Sound Transmission Class Ratings of Concrete Masonry Walls, TEK 13-01D. Concrete Masonry & Hardscapes Association, 2012.
Standard Test Method for Sound Absorption and Sound Absorption Coefﬁcients by the Reverberation Room Method, ASTM C423-07. ASTM International, 2007.
Standard Method for Determining the Sound Transmission Class Rating for Masonry Walls, TMS 0302-07. The Masonry Society, 2007.

TEK 13-02A, Revised 2007. CMHA and the companies disseminating this technical information disclaim any and all responsibility and liability for the accuracy and the application of the information contained in this publication.