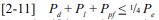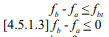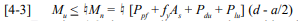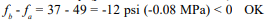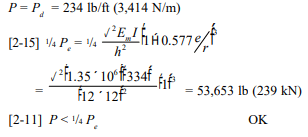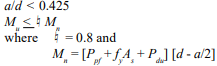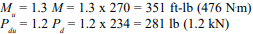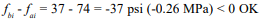Home / Technical Resources / post-tensioned masonry

Resources

Creep Properties of Post-Tensioned and High-Rise Concrete Masonry

August 2018

INTRODUCTION

Time dependent deformations such as creep are generally only designed for in prestressed (post-tensioned) concrete masonry and high-rise loadbearing masonry buildings. Ordinary concrete masonry units with grout-filled cores and steel reinforcement and designs based on well known engineering principles have been used extensively in loadbearing concrete masonry up to 20 stories in height without analysis for creep. However, as concrete masonry is used for increasingly large and tall buildings, consideration of the time-dependent deformations that occur becomes more important.

Creep is proportional to masonry dimensions and applied stress and therefore increases as height and loads increase. Prestressing (post-tensioning) of concrete masonry is another relatively new innovation where the creep properties must be taken into consideration. This procedure involves the introduction compressive forces into the masonry using prestressing tendons in order to place the masonry into a compressive mode where it is most effective.

Due to the relatively recent advent of these specialized construction procedures, creep properties of masonry have been actively studied only in the last 25 years. Much of the information prior to this was based on the documented properties of concrete. Although the properties of the two are similar, concrete masonry is composed of hollow, cementitious units that are substantially cured at the time of placement and mortar which is plastic at the time of placement. This makes the time-dependent properties somewhat different from concrete.

The majority of the effects of creep occur within the first three to five years (ref. 9). The effects are most dramatic within the first 30 days and about 90% complete at the end of the first year. The effect of these deformations on concrete masonry if they are not designed for is the potential for undesirable cracking.

TOTAL TIME-DEPENDENT DEFORMATIONS

Creep and shrinkage are deformations that occur over time and must be addressed in these specialized construction processes. There are two forms of shrinkage. 1). Drying shrinkage refers to the shrinkage that occurs as the moisture content of the masonry assemblage decreases over time. 2). Carbonation shrinkage is the reaction between the cementitious materials in the masonry and carbon dioxide in the atmosphere. Shrinkage properties are discussed extensively in CMHA’s CMU-TEC-009-23 Crack Control Strategies for Concrete Masonry Construction (ref. 4).

In research, creep is determined by measuring the total deformation on a loaded specimen and the shrinkage effects on a companion “control” specimen not subjected to loading. The creep then is determined by taking the difference in the two values.

One of the first of these studies was conducted in 1976 sponsored by the Portland Cement Association laboratories and the Concrete Masonry & Hardscapes Association to ascertain the technical and economical feasibility of constructing reinforced concrete masonry buildings as high as 50 stories (ref. 7). The research was to determine the engineering properties of the very high strength materials that would be required under the heavy sustained loading. Since that time a number of other studies have been conducted, particularly in regard to prestressed masonry construction (ref. 1, 2, 6, 7, 9, 10, 12).

CREEP

Creep refers to the increase in strain over time that occurs under sustained constant load. The deformations due to creep are normally three to five times the amount of the initial strain for concrete masonry most of which occurs within 1 year of constant stress (ref. 5). Mortar has a higher proportionate amount of creep than concrete masonry units. Even though mortar joints make up only about 7% of the area of a wall, they typically account for about 20% of the creep (ref. 10). The final creep value of masonry increases with increasing proportion of mortar.

Creep of concrete masonry is influenced by several factors:

Unit Strength – Creep is reduced when higher strength units are used (ref. 10).
Type of Mortar – Creep is reduced when higher strength mortar is used (ref 10).
Percentage of Reinforcement – The presence of reinforcement reduces creep as it helps to carry some of the vertical load (ref. 2).
Relative Humidity – The effect of relative humidity is slight on creep, however, creep tends to increase with an increase moisture content (ref. 1).
Level of Stress – Creep of concrete masonry is proportional to stress (ref. 1 5, 7, 10).
Age at loading – Research indicates that creep is reduced for masonry subjected to stress after 14 days of age (ref. 1, 2, 5, 7, 9). Schubert proposes that “the influence of the age at loading is slight from a masonry age of about 2 weeks onwards, as there is only a slight increase in the strength of both units and mortar after this time” (ref. 9).
Pore Structure – An increase in pore structure of unit and mortar tends to increase creep (ref. 10).
Aggregate Type – Little difference was found in the amount of creep between lightweight and normal weight aggregate (ref. 1, 7) and in some cases lightweight exhibited less creep (ref. 1). However, the total deformation of lightweight concrete masonry typically is greater due to the higher initial deformation.

More recent research on more conventionally strengthed concrete masonry ( f’m of 1500 psi) (10.34 MPa) produced values of creep somewhat higher (ref. 1, 10). Based on his research, Badger (ref. 1) recommends a value of 13 x 10-7 per psi (1.87 x 10-4 per MPa) for concrete masonry. The average tested prism strength was 2080 psi (14.34 MPa) for the normal weight prisms and 1580 psi (10.89 MPa) for the lightweight. Sustained stress levels of 0, 50, 150, and 250 psi (0, 0.34, 1.03, and 1.72 MPa) were applied for a period of 300 days. Test results are as shown in Figures 2 through 5. The negative creep indicated for the first 100 days in Figures 4 & 5 is not really happening. It is an aberration attributed to the more rapid drying shrinkage of the control specimens due to open cores at the top whereas the loaded specimens were covered by the loading plate. This allowed the control specimens to dry out from the inside as well as the outside as opposed to the loaded specimens which dried from the outside only.

Schultz and Scolforo (ref. 10) recommend a creep coefficient of 2.5 for Type M mortar and 4 for Type N mortar based their research. As indicated earlier, this is the ratio of creep to the amount of initial strain. The corresponding specific creep coefficient is obtained by simply dividing the creep coefficient by the modulus of elasticity. For 1500 f’_m and a creep coefficient of 2.5, the specific creep coefficient k_c then becomes 18.5 x 10^-7 per psi (2.68 x 10^-5 per MPa). A 2500 f’_m with Type M mortar results in a k_c of 11.1 x 10^-7 per psi (16.1 x 10^-5 per MPa). Since the modulus of elasticity is a function of the specified masonry strength f’_m, this approach makes creep dependent on both mortar strength and masonry strength.

Figure 1—Time Dependent Strains in High Strength Lightweight and Normal Weight Block Prisms (ref. 7)

Prestressed Concrete Masonry

Creep is of particular importance in prestressed concrete masonry where it contributes to prestress losses. Prestressed concrete masonry typically involves the application of compressive stresses by a prestressing tendon to a masonry wall prior to application of the building loads. This compressive stress counteracts the applied tensile stress and increases shear capacity, providing an economical alternative to traditional reinforcement. Creep loss in prestressed masonry occurs when the prestressing tendon shortens with the masonry (ref. 1) and must be accounted for in the design. This differs from mild reinforcement which helps to minimize creep by carrying some of the load as opposed to prestressing which adds to the load carried by the masonry. Consequently creep associated with prestressed masonry is typically higher than that of reinforced masonry.

Fairly accurate estimates of creep in prestressed masonry are needed as overestimating the creep may contribute to overstressing the wall in compression when it is fully loaded. Underestimating creep can result in the wall having less available capacity than assumed which can lead to tensile cracking. Historically, in practice for concrete masonry it has been found that the sum of individual component losses determined by approved methods average between 30 to 35% of the total prestress force. This is often used as a check to ensure that all of the prestress losses are accurately accounted for.

CONCLUSIONS

Creep generally only needs to be considered in loadbearing concrete masonry high-rise buildings or in prestressed masonry construction to determine the prestress losses. Factors to consider to minimize the amount and rate of creep are as follows:

Allow units to dry for a period (at least 14 days) after manufacture and before placing to limit creep and initial deformation due to drying shrinkage.
Prior to the application of super-imposed loads, cure completed concrete masonry by fogging or other acceptable means to reduce the rate and amount of creep when possible.
Increasing the amount of vertical mild reinforcement tends to decrease creep.
Creep is reduced when higher strength units and mortar are used.
Creep is more pronounced within the first 14 days of placement of masonry.
Research indicates that creep in lightweight and normal weight concrete masonry are about the same.
In high-rise buildings, the absolute shortening of the walls should not be critical, provided that all members are shortening about the same amount. This can be achieved by using walls containing similar percentages of reinforcing steel and by ensuring that all walls are subjected to similar stresses. The effects of differential shortening on continuous floor slabs can be minimized by using long spans (ref 7).

REFERENCES

Badger, C. C.R., “Creep of Prestressed Concrete Masonry”. Thesis submitted to Department of Civil Engineering at The University of Wyoming, August 1997.
Ben-Omran, H., Glanville, J. I., and Hatzinikolas, M. A., “Effects of Time-Dependent Deformations on the Behavior of Reinforced Masonry Columns”, TMS Journal, February 1994.
Building Code Requirements for Masonry Structures, ACI 530-99 / ASCE 5-99 / TMS 402-99. Reported by the Masonry Standards Joint Committee, 1999.
Crack Control Strategies for Concrete Masonry Construction, CMU-TEC-009-23, Concrete Masonry & Hardscapes Association, 2023..
Drysdale, R. G., Hamid, A. A., and Baker, L. R., Masonry Structures: Behavior and Design. Prentice Hall, Inc., 1999.
Forth, J. P., Bingel, P.R., and Brooks, J. J., “Influence of Age at Loading on Long-Term Movements of Clay Brick and Concrete Block Masonry”, Proceedings, Seventh North American Masonry Conference, June 1996.
Helgason, T. and Russell, H. G., High Strength Reinforced Concrete Masonry Walls. Portland Cement Association, May 1976.
Post-Tensioned Concrete Masonry Wall Design, TEK 1420A, Concrete Masonry & Hardscapes Association, 2002.
Schubert, P., “Strength and Deformation Properties of Masonry Made From Lightweight Concrete Units”, Proceedings, Sixth Canadian Symposium, June 1992.
Schultz, A. E. and Scolforo, M. J., “Engineering Design Provisions for Prestressed Masonry Part 2: Steel Stresses and Other Considerations”, TMS Journal, February, 1992.
Van der Pluijm, R. and Vermeltfoort, A., “Influence of the Type of Mortar Joint on the Time Dependent Behaviour of Masonry”, Proceedings, Eighth Canadian Masonry Symposium, May, 1998.

Post-Tensioned Concrete Masonry Wall Design

August 2018

INTRODUCTION

The 1999 Building Code Requirements for Masonry Structures, ACI 530/ASCE 5/TMS 402 (ref. 1), was the first masonry code in the United States to include general design provisions for prestressed masonry. Prestressing masonry is a process whereby internal compressive stresses are introduced to counteract tensile stresses resulting from applied loads. Compressive stresses are developed within the masonry by tensioning a steel tendon, which is anchored to the top and bottom of the masonry element (see Figure 1). Post-tensioning is the primary method of prestressing, where the tendons are stressed after the masonry has been placed. This TEK focuses on the design of concrete masonry walls constructed with vertical post-tensioned tendons.

Advantages

Prestressing has the potential to increase the flexural strength, shear strength and stiffness of a masonry element. In addition to increasing the strength of an element, prestressing forces can also close or minimize the formation of some cracks. Further, while research (refs. 14, 15) indicates that ductility and energy dissipation capacity are enhanced with prestressing, Building Code Requirements for Masonry Structures (ref. 1) conservatively does not take such performance into account.

Post-tensioned masonry can be an economical alternative to conventionally reinforced masonry. One major advantage of prestressing is that it allows a wall to be reinforced without the need for grout. Also, the number of prestressing tendons may be less than the number of reinforcing bars required for the same flexural strength.

Post-tensioning masonry is primarily applicable to walls, although it can also be used for beams, piers, and columns. Vertical post-tensioning is most effective for increasing the structural capacity of elements subjected to relatively low axial loads. Structural applications include loadbearing, nonloadbearing and shear walls of tall warehouses and gymnasiums, and commercial buildings, as well as retaining walls and sound barrier walls. Post-tensioning is also an option for strengthening existing walls.

Figure 1—Schematic of Typical Post-Tensioned Wall

MATERIALS

Post-tensioned wall construction uses standard materials: units, mortar, grout, and perhaps steel reinforcement. In addition, post-tensioning requires tendons, which are steel wires, bars or strands with a higher tensile strength than conventional reinforcement. Manufacturers of prestressing tendons must supply stress relaxation characteristics for their material if it is to be used as a prestressing tendon. Specifications for those materials used specifically for post-tensioning are given in Table 1. Other material specifications are covered in references 9 through 12. Construction is covered in Post-Tensioned Concrete Masonry Wall Construction, TEK 03-14 (ref. 3).

CORROSION PROTECTION

As with conventionally reinforced masonry structures, Building Code Requirements for Masonry Structures (ref. 1) mandates that prestressing tendons for post-tensioned masonry structures be protected against corrosion. As a minimum, the prestressing tendons, anchors, couplers and end fittings in exterior walls exposed to earth or weather must be protected. All other walls exposed to a mean relative humidity exceeding 75% must also employ some method of corrosion abatement. Unbonded tendons can be protected with galvanizing, epoxy coating, sheathing or other alternative method that provides an equivalent level of protection. Bonded tendons are protected from corrosion by the corrugated duct and prestressing grout in which they are encased.

DESIGN LOADS

As for other masonry structures, minimum required design loads are included in Minimum Design Loads for Buildings and Other Structures, ASCE 7 (ref. 5), or the governing building codes. If prestressing forces are intended to resist lateral loads from earthquake, a factor of 0.9 should be applied to the strength level prestress forces (0.6 for allowable stress design) as is done with gravity loads.

STRUCTURAL DESIGN

The design of post-tensioned masonry is based on allowable stress design procedures, except for laterally restrained tendons which use a strength design philosophy. Building Code Requirements for Masonry Structures (ref. 1) prescribes allowable stresses for unreinforced masonry in compression, tension and shear, which must be checked against the stresses resulting from applied loads.

The flexural strength of post-tensioned walls is governed by either the flexural tensile stress of the masonry (the flexural stress minus the post-tensioning and dead load stress), the masonry compressive stress, the tensile stress within the tendon, the shear capacity of the masonry or the buckling capacity of the wall.

Masonry stresses must be checked at the time of peak loading (independently accounting for both short-term and long-term losses), at the transfer of post-tensioning forces, and during the jacking operation when bearing stresses may be exceeded. Immediately after transfer of the post-tensioning forces, the stresses in the steel are the largest because long-term losses have not occurred. Further, because the masonry has had little time to cure, the stresses in the masonry will be closer to their capacity. Once long-term losses have transpired, the stresses in both the masonry and the steel are reduced. The result is a coincidental reduction in the effective capacity due to the prestressing force and an increase in the stresses the fully cured masonry can resist from external loads.

Effective Prestress

Over time, the level of prestressing force decreases due to creep and shrinkage of the masonry, relaxation of the prestressing tendons and potential decreases in the ambient temperature. These prestressing losses are in addition to seating and elastic shortening losses witnessed during the prestressing operation. In addition, the prestressing force of bonded tendons will decrease along the length of the tendon due to frictional losses. Since the effective prestressing force varies over time, the controlling stresses should be checked at several stages and loading conditions over the life of the structure.

The total prestress loss in concrete masonry can be assumed to be approximately 35%. At the time of transfer of the prestressing force, typical losses include: 1% seating loss + 1% elastic shortening = 2%. Additional losses at service loads and moment strength include:

relaxation	3%
temperature	10%
creep	8%
CMU shrinkage	7%
contingency	5%
total	33%

Prestress losses need to be estimated accurately for a safe and economical structural design. Underestimating losses will result in having less available strength than assumed. Overestimating losses may result in overstressing the wall in compression.

Effective Width

In theory, a post-tensioning force functions similarly to a concentrated load applied to the top of a wall. Concentrated loads are distributed over an effective width as discussed in the commentary on Building Code Requirements for Masonry Structures (ref. 1). A general rule-of-thumb is to use six times the wall thickness as the effective width.

Elastic shortening during post-tensioning can reduce the stress in adjacent tendons that have already been stressed. Spacing the tendons further apart than the effective width theoretically does not reduce the compressive stress in the effective width due to the post-tensioning of subsequent tendons. The applied loads must also be consolidated into the effective width so the masonry stresses can be determined. These stresses must be checked in the design stage to avoid overstressing the masonry.

Flexure

Tensile and compressive stresses resulting from bending moments applied to a section are determined in accordance with conventional elastic beam theory. This results in a triangular stress distribution for the masonry in both tension and compression. Maximum bending stress at the extreme fibers are determined by dividing the applied moment by the section modulus based on the minimum net section.

Net Flexural Tensile Stress

Sufficient post-tensioning force needs to be provided so the net flexural tensile stress is less than the allowable values. Flexural cracking should not occur if post-tensioning forces are kept within acceptable bounds. Flexural cracking due to sustained post-tensioning forces is believed to be more severe than cracking due to transient loading. Flexural cracks due to eccentric post-tensioning forces will remain open throughout the life of the wall, and may create problems related to water penetration, freeze-thaw or corrosion. For this reason, Building Code Requirements for Masonry Structures (ref. 1) requires that the net flexural tensile stress be limited to zero at transfer of the post-tensioning force and for service loadings with gravity loads only.

Axial Compression

Compressive stresses are determined by dividing the sum of the post-tensioning and gravity forces by the net area of the section. They must be less than the code prescribed (ref. 1) allowable values of axial compressive stress.

Walls must also be checked for buckling due to gravity loads and post-tensioning forces from unrestrained tendons. Laterally restrained tendons can not cause buckling; therefore only gravity compressive forces need to be checked for buckling in walls using laterally restrained tendons. Restraining the tendons also ensures that the tendons do not move laterally in the wall when the masonry deflects. The maximum compressive force that can be applied to the wall based upon ¼ buckling is P_e, per equation 2-11 of Building Code Requirements for Masonry Structures (ref. 1).

Combined Axial and Flexural Compressive Stress

Axial compressive stresses due to post-tensioning and gravity forces combine with flexural compressive stresses at the extreme fiber to result in maximum compressive stress. Conversely, the axial compressive stresses combine with the flexural tensile stresses to reduce the absolute extreme fiber stresses. To ensure the combination of these stresses does not exceed code prescribed allowable stresses, a unity equation is checked to verify compliance. Employing this unity equation, the sum of the ratios of applied-to-allowable axial and flexural stresses must be less than one. Unless standards (ref. 5) limit its use, an additional one-third increase in allowable stresses is permitted for wind and earthquake loadings, as is customary with unreinforced and reinforced masonry. Further, for the stress condition immediately after transfer of the post-tensioning force, a 20% increase in allowable axial and bending stresses is permitted by Building Code Requirements for Masonry Structures (ref. 1).

Shear

As with all stresses, shear stresses are resisted by the net area of masonry, and the wall is sized such that the maximum shear stress is less than the allowable stress. In addition, the compressive stress due to post-tensioning can be relied on to increase allowable shear stresses in some circumstances.

Post-Tensioning Tendons

The stress in the tendons is limited (ref. 1) such that:

the stress due to the jacking force does not exceed 0.94f_py, 0.80f_pu, nor that recommended by the manufacturer of the tendons or anchorages,
the stress immediately after transfer does not exceed 0.82f_py nor 0.74f_pu, and
the stress in the tendons at anchorages and couplers does not exceed 0.78f_py nor 0.70f_pu.

DETERMINATION OF POST-TENSIONING FORCES

Case (a) after prestress losses and at peak loading:

Assuming that the moment, M, due to wind or earthquake loadings is large relative to the eccentric load moment, the critical location will be at the mid-height of the wall for simply-supported walls, and the following equations apply (bracketed numbers are the applicable Building Code Requirements for Masonry Structures (ref. 1) equation or section numbers):

The 1.33 factor in Equation [2-10] represents the one- third increase in allowable stress permitted for wind and earthquake loadings. If the moment, M, is a result of soil pressures (as is the case for retaining walls), the 1.33 factor in Equation [2-10] must be replaced by 1.00.

Note that if the tendons are laterally restrained, P_pf should not be included in Equation [2-11].

(under the load combination of prestressing force and dead load only)

Additional strength design requirements for laterally restrained tendons:

Equation 4-3 above applies to members with uniform width, concentric reinforcement and prestressing tendons and concentric axial load. The nominal moment strength for other conditions should be determined based on static moment equilibrium equations.

Case (b) at transfer of post-tensioning:

Assuming that vertical live loads are not present during post-tensioning, the following equations apply. The worst case is at the top of the wall where post-tensioning forces are applied.

For cantilevered walls, these equations must be modified to the base of the wall.

If the eccentricity of the live load, P_l, is small, neglecting the live load in Equation [2-10] may also govern.

Case (c) bearing stresses at jacking:

Bearing stresses at the prestressing anchorage should be checked at the time of jacking. The maximum allowable bearing stress at jacking is 0.50f’_mi per Building Code Requirements for Masonry Structures (ref. 1) section 4.9.4.2.

DESIGN EXAMPLE

Design a simply-supported exterior wall 12 ft (3.7 m) high for a wind load of 15 psf (0.72 kPa). The wall is constructed of concrete masonry units complying with ASTM C 90 (ref. 6). The units are laid in a full bed of Type S Portland cement lime mortar complying with ASTM C 270 (ref. 7). The specified compressive strength of the masonry (f’_m) is 1,500 psi (10.3 MPa). The wall will be post-tensioned with ⁷/₁₆ in. (11 mm) diameter laterally restrained tendons when the wall achieves a compressive strength of 1,250 psi (8.6 MPa). Axial load and prestress are concentric.

Given:
8 in. (203 mm) CMU
t_f = 1.25 in. (32 mm)
f’_m = 1,500 psi (10.3 MPa)
f’_mi = 1,250 psi (8.6 MPa)
F_bt = 25 psi (0.17 MPa) (Type S Portland cement/lime mortar)
f_py = 100 ksi (690 MPa) (bars)
f_pu = 122 ksi (840 MPa)
A_ps = 0.14 in² (92 mm²)
E_s = 29 x 10⁶ psi (200 GPa)
E_m = 900 f’_m = 1.35 x 10⁶ psi (9,300 MPa)
n = E_s/E_m = 21.5
d = 7.625/2 in. = 3.81 in. (97 mm) (tendons placed in the center of the wall)
unit weight of CMU wall = 39 psf (190 kg/m²) (ref. 13)

Loads: M = wh²/8 = (15)(12)²/8 = 270 ft-lb (366 N-m)
P_d at mid-height = (39)(12)/2 = 234 lb/foot of wall (3,410 N/m) (P_l = 0)

Maximum tendon stresses:
Determine governing stresses based on code limits (ref. 1):

At jacking:	0.94 f_py = 94.0 ksi (648 MPa)
	0.80 f_pu = 97.6 ksi (673 MPa)
At transfer:	0.82 f_py = 82.0 ksi (565 MPa)
	0.74 f_pu = 90.3 ksi (623 MPa)
At service loads:	0.78 f_py = 78.0 ksi (538 MPa) ⇒ governs
	0.70 f_pu = 85.4 ksi (589 MPa)

Because the tendon’s specified tensile strength is less than 150 ksi (1,034 MPa), f_ps = f_se (per ref. 1 section 4.5.3.3.4).

Prestress losses: Assume 35% total loss (as described in the Effective Prestress section above).

Tendon forces:
Determine the maximum tendon force, based on the governing tendon stress determined above for each case of jacking, transfer and service. At transfer, include 2% prestress losses. At service, include the full 35% losses.
Tendon capacity at jacking = 0.94 f_pyA_ps = 13.3 kips (59 kN)
Tendon capacity at transfer = 0.82 f_pyA_ps A x 0.98 = 11.4 kips (51 kN) (including transfer losses)
Tendon capacity at service = 0.78 f_pyA_ps A x 0.65 = 7.2 kips (32 kN) (including total losses)

Try tendons at 48 in. (1,219 mm) on center (note that this tendon spacing also corresponds to the maximum effective prestressing width of six times the wall thickness).

Determine prestressing force, based on tendon capacity determined above:
at transfer: P_pi = 11.4 kips/4 ft = 2,850 lb/ft (41.6 kN/m)
at service: P_pf = 7.2 kips/4 ft = 1,800 lb/ft (26.3 kN/m)

Wall section properties: (ref. 8)
8 in. (203 mm) CMU with full mortar bedding:
A_n = 41.5 in.²/ft (87,900 mm²/m)
I = 334 in.⁴/ft (456 x 10⁶ mm⁴/m)
S = 87.6 in.³/ft (4.71 x 10⁶ mm³/m)
r = 2.84 in. (72.1 mm)

At service loads:
At service, the following are checked: combined axial compression and flexure using the unity equation (equation 2-10); net tension in the wall; stability by ensuring the compressive load does not exceed one-fourth of the buckling load, P_e, and shear and moment strength.

Check combined axial compression and flexure:

Check tension for load combination of prestress force and dead load only (per ref. 1 section 4.5.1.3):

Check stability:
Because the tendons are laterally restrained, the prestressing force, P_pf, is not considered in the determination of axial load ( per ref. 1 section 4.5.3.2), and the wall is not subject to live load in this case, so equation 2-11 reduces to:

Check moment strength:
Building Code Requirements for Masonry Structures section 4.5.3.3 includes the following criteria for moment strength of walls with laterally restrained tendons:

In addition, the compression zone must fall within the masonry, so a < t_f.

where 1.3 and 1.2 are load factors for wind and dead loads, respectively.

At transfer:
Check combined axial compression and flexure using the unity equation (equation 2-10) and net tension in the wall.

Check tension for load combination of prestress force and dead load only (per ref. 1 section 4.5.1.3):

Therefore, use ⁷/₁₆ in. (11 mm) diameter tendons at 48 in. (1,219 mm) o.c. Note that although wall design is seldom governed by out-of-plane shear, the shear capacity should also be checked.

NOTATIONS

A_n net cross-sectional area of masonry section, in.² (mm²)
A_ps threaded area of post-tensioning tendon, in.² (mm²)
A_s cross-sectional area of mild reinforcement, in.² (mm²)
a depth of an equivalent compression zone at nominal strength, in. (mm)
b width of section, in. (mm)
d distance from extreme compression fiber to centroid of prestressing tendon, in. (mm)
E_s modulus of elasticity of prestressing steel, psi (MPa)
E_m modulus of elasticity of masonry, psi (MPa)
e_d eccentricity of dead load, in. (mm)
e_l eccentricity of live load, in. (mm)
e_p eccentricity of post-tensioning load, in. (mm)
F_a allowable masonry axial compressive stress, psi (MPa)
F_ai allowable masonry axial compressive stress at transfer, psi (MPa)
F_b allowable masonry flexural compressive stress, psi (MPa)
F_bi allowable masonry flexural compressive stress at transfer, psi (MPa)
F_bt allowable flexural tensile strength of masonry, psi (MPa)
f_a axial stress after prestress loss, psi (MPa)
f_ai axial stress at transfer, psi (MPa)
f_b flexural stress after prestress loss, psi (MPa)
f_bi flexural stress at transfer, psi (MPa)
f’_m specified compressive strength of masonry, psi (MPa)
f’_mi specified compressive strength of masonry at time of transfer of prestress, psi (MPa)
f_ps stress in prestressing tendon at nominal strength, psi (MPa)
f_pu specified tensile strength of prestressing tendon, ksi (MPa)
f_py specified yield strength of prestressing tendon, ksi (MPa)
f_se effective stress in prestressing tendon after all pre-stress losses have occurred, psi (MPa)
f_y specified yield strength of steel for reinforcement and anchors, psi (MPa)
h masonry wall height, in. (mm)
I moment of inertia of net wall section of extreme fiber tension or compression, in.⁴/ft (mm⁴/m)
M moment due to lateral loads, ft-lb (N⋅m)
M_n nominal moment strength, ft-lb (N⋅m)
M_u factored moment due to lateral loads, ft-lb (N⋅m)
n modular ratio of prestressing steel and masonry (E_s/E_m)
P_d axial dead load, lb/ft (kN/m)
P_du factored axial dead load, lb/ft (kN/m)
P_e Euler buckling load, lb/ft (kN/m)
P_l axial live load, lb/ft (kN/m)
P_lu factored axial live load, lb/ft (kN/m)
P_pi prestress force at transfer, lb/ft (kN/m)
P_pf prestress force including losses, lb/ft (kN/m)
r radius of gyration for net wall section, in. (mm)
S section modulus of net cross-sectional area of the wall, in.³ /ft (mm³/m)
t_f face shell thickness of concrete masonry, in. (mm)
w applied wind pressure, psf (kPa)
¤ strength reduction factor = 0.8

REFERENCES

Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
Building Code Requirements for Structural Concrete, ACI 318-99. Detroit, MI: American Concrete Institute, Revised 1999.
Construction of Post-Tensioned Concrete Masonry Walls, TEK 03-14. Concrete Masonry & Hardscapes Association, 2002.
International Building Code. International Code Council, 2000.
Minimum Design Loads for Buildings and Other Structures, ASCE 7-98, American Society of Civil Engineers, 1998.
Standard Specification for Loadbearing Concrete Masonry Units, ASTM C 90-01a. American Society for Testing and Materials, 2001.
Standard Specification for Mortar for Unit Masonry, ASTM C 270-01. American Society for Testing and Materials, 2001.
Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.
Concrete Masonry Unit Shapes, Sizes, Properties, and Specifications, CMU-TEC-001-23, Concrete Masonry & Hardscapes Association, 2023.
Mortars for Concrete Masonry, TEK 09-01A. Concrete Masonry & Hardscapes Association, 2001.
Grout for Concrete Masonry, TEK 09-04. Concrete Masonry & Hardscapes Association, 2005.
Steel for Concrete Masonry Reinforcement, TEK 12-04D. Concrete Masonry & Hardscapes Association, 1998.
Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.
Schultz, A.E., and M.J. Scolforo, An Overview of Prestressed Masonry, TMS Journal, Vol. 10, No. 1, August 1991, pp. 6-21.
Schultz, A.E., and M.J. Scolforo, Engineering Design Provisions for Prestressed Masonry, Part 1: Masonry Stresses, Part 2: Steel Stresses and Other Considerations, TMS Journal, Vol. 10, No. 2, February 1992, pp. 29-64.
Standard Specification for Steel Strand, Uncoated Seven-Wire for Prestressed Concrete, ASTM A 416-99. American Society for Testing and Materials, 1999.
Standard Specification for Uncoated Stress-Relieved Steel Wire for Prestressed Concrete, ASTM A 421-98a. American Society for Testing and Materials, 1998.
Standard Specification for Uncoated High-Strength Steel Bar for Prestressed Concrete, ASTM A 722-98. American Society for Testing and Materials, 1998.
Standard Specification for Compressible-Washer-Type Direct Tension Indicators for Use with Structural Fasteners, ASTM F 959-01a. American Society for Testing and Materials, 2001.

Post-Tensioned Concrete Masonry Wall Construction

August 2018

INTRODUCTION

Prestressing is the general term used when a structural element is compressed prior to being subjected to building loads. This initial state of compression offsets tensile stresses from applied loads. Post-tensioning is a specific method of prestressing where tendons are stressed after the wall has been placed. The other type of prestressing, called pretensioning, involves tensioning the tendon prior to construction of the masonry. Because virtually all prestressed masonry built to date has been post-tensioned, the two terms are often used interchangeably as they apply to this form of masonry design and construction.

Post-tensioned concrete masonry walls have been built for schools, retail, manufacturing, highway sound barriers, warehouses and other types of structures. In addition, posttensioning has been used to strengthen and repair existing masonry walls. This TEK addresses new concrete masonry walls laid in running bond and built with unbonded vertical posttensioning tendons. Post-Tensioned Concrete Masonry Wall Design, TEK 14-20A (ref. 1) addresses the structural design of vertically post-tensioned walls.

POST-TENSIONING

In post-tensioned construction, hollow concrete masonry units are laid conventionally and prestressing tendons are either placed in the concrete masonry cells or in the cavity between multiple wythes. Current design codes (ref. 3) typically address post-tensioning of masonry walls laid in running bond. The cells or cavity containing the tendons may or may not be grouted. Grouting helps increase cross-sectional area for shear and compressive resistance, but increases construction cost and time.

Prestressing tendons are either installed during wall construction, or access ports are left in the walls so the tendons can be slipped in after the walls are completed. In either case, the tendons are tensioned only after the walls have cured for approximately three to seven days.

MATERIALS

Construction of a post-tensioned wall proceeds similarly to that of conventional masonry. The materials are the same, with the addition of hardware to develop the posttensioning forces, steel prestressing tendons which can be wires, bars or strands, and sometimes prestressing grout.

Concrete Masonry Units

Open-ended (Aand H-shaped) concrete masonry units (Figure 1) are particularly suited to post-tensioned masonry, as these units can be placed around the tendons without having to lift the units over the tendons. While these two-core units are commonly used, proprietary units are also being developed that are specifically intended for use with tendons.

The net area strength of concrete masonry units must be at least 1,900 psi (13.1 MPa) per Standard Specification for Loadbearing Concrete Masonry Units (ref. 2). However, stronger units are often specified for post-tensioned walls to utilize the higher compressive strength.

Mortar and Grout

Type S mortar is commonly used for conventional loadbearing masonry, and Type S is a good choice for posttensioned masonry as well. Higher early strength mortars can accommodate earlier stressing.

Because mortar must be placed on concrete masonry webs adjacent to grouted cores to contain the fluid grout, full mortar bedding is sometimes specified when grout is used. Mortar bedding is a design issue as well, as the section properties of a wall with face shell mortar bedding are different from those of a fully bedded wall.

Because this TEK addresses unbonded tendons only, the grout discussed here is conventional grout (ASTM C 476, ref. 6), not prestressing grout. Prestressing grout is only used with bonded tendons. Encasing tendons in conventional grout restrains the tendons, but they are still considered unbonded.

Tendons

In the United States, tendons are usually high-strength bars joined by couplers, although Building Code Requirements for Masonry Structures (ref. 3) also allows steel strands or wires to be used. Couplers allow the use of shorter bars which minimizes the height of lifting. To date, there are no code provisions for tendons which are not steel.

Important features of the tendons are their size, strength, and relaxation characteristics. Most tendons currently available in the United States are bars between 7/16 and 1 in. (11 and 25 mm) in diameter, with strengths between 60,000 and 100,000 psi (413 and 690 MPa), depending on the supplier. Steel strand tendons are generally 270,000 psi (1,860 MPa). Tendons are usually placed in hollow cells of masonry units with little or no grouting, except for certain shear walls (these must be identified on the design drawings). In addition, the open-ended units shown in Figure 1 must be grouted to meet minimum web requirements in ASTM C 90 (ref. 2).

Tendon Corrosion Protection

Tendons must be protected from moisture deterioration, and the design documents should indicate the type of protection required. Tendons in walls with a likelihood of high moisture levels (single wythe exterior walls in areas of high humidity and interior walls around swimming pools, locker rooms, etc.) must have corrosion protection in addition to that provided by the masonry cover, such as hot-dipped galvanizing (ref. 3). In practice, most prestressing tendons are supplied with a hotdipped galvanized coating. It is considered good practice to use additional corrosion protection, such as flexible epoxy-type coatings, for tendons in moist environments.

Grouting

While the need for grouting is minimized compared to conventionally reinforced walls, grout is still needed for mild reinforcement, anchorages for the tendons, such as in bond beams, and tendon restraints.

Anchorages

Each tendon is anchored at the foundation and extends to the top of the wall. Building Code Requirements for Masonry Structures (ref. 3) requires that tendons be anchored by mechanical embedments or bearing devices or by bond development in concrete. Tendons can not be anchored by bond development into the masonry. The foundation anchorage is embedded in the wall or footing while the top anchorage utilizes a special block, a precast concrete spreader beam or a grouted bond beam.

Unless the design documents call out specific bottom anchors, the contractor must select the anchor appropriate to the conditions. The cast-in-place bottom anchor (Figure 2a) is preferred for shear walls and for fire walls. While they are the best anchors for capacity, cast-in-place anchors are the most difficult to align. Cast-in-place anchors are often set by the foundation contractor, not the mason. Thus, quality control is a concern with these anchors.

The mason controls bottom anchor placement when either adhesive anchors are installed in the foundation (Figure 2c), or when an anchor is used which does not rely on the foundation for support (Figure 2b). If the anchor in Figure 2b is used, foundation dowels are grouted into the wall to lock it in place. In some instances, tendons can also begin at an upper floor and not at the foundation. In this case, the foundationless anchor is used with a bond beam, similar to Figure 2b.

The mechanical post-installed anchors can be used for nearly all applications, while the adhesive type should not be used for fire walls.

CONSTRUCTION

Key steps of post-tensioning concrete masonry walls include: selecting and setting the bottom anchorages; installing the tendons; selecting and setting the top anchorages; and a tensioning the tendons.

Bottom Anchors

Bottom anchors are most critical to the proper construction of post-tensioned walls. Alignment is essential to ensure that the tendons are placed exactly as intended.

Tendons

Tendons are usually placed concentric with the wall. However, they may be placed off-center to counteract bending moments due to eccentric vertical forces or lateral forces from a single direction. However, tendons should not be placed such that tensile stresses develop in the wall due to the combination of prestressing force and dead load.

Laterally-unrestrained tendons are free to move within the cell or cavity and are the simplest to construct. Laterally restrained tendons are not free to move within a cell or cavity. Restraint is accomplished by grouting the full height of the tendon or by providing intermittent restraints—either grout plugs or mechanical restraints—at the quarter points of the wall height.

Placing tendons is much like that of mild reinforcement. They may be installed after the masonry is constructed provided the design allows laterally-unrestrained tendons. If laterally restrained tendons are required, the tendon placement should proceed simultaneously with the masonry to allow the restraints to be installed unless the cells will be grouted.

Tendon positioners (see Figure 3) are useful to maintain the tendon location within the wall during construction of the masonry. Positioners may also function as restraints if their capacity is determined by testing.

In all details, the tendons must be able to slip freely. If grout encases the tendon either totally or at restraints or bond beams, a bond breaker such as poly tape should be used to allow the tendon to slip.

Tendons can also be either bonded or unbonded. Bonded tendons are encapsulated by prestressing grout in a corrugated duct which is bonded to the surrounding masonry by grout. Both the prestressing grout inside the duct and the grout around the duct must be cured before the tendons are stressed. Thus, bonded tendons are also laterally-restrained. All other tendons are unbonded. However, unbonded tendons may be either laterally-restrained or unrestrained. Walls with laterally unrestrained and unbonded tendons do not require grouting and are generally the most economical to construct. However, the wall performance will not be as good as with laterally restrained tendons. The designer must specify which system will be used.

For some conditions, primarily seismic, grouted conventional reinforcement is used in addition to post-tensioning tendons to provide minimum requirements of bonded reinforcement. However, post-tensioned walls are most economical when the grouting is minimized or eliminated totally in comparison to a conventionally reinforced wall. The higher cost of the post-tensioning materials is more than offset by the savings of placing fewer tendons compared to reinforcing bars and eliminating most of the grouting.

Top Anchors

The top anchor must be placed on solid masonry, a grouted bond beam or a precast concrete unit. The anchor should not be supported by mortar.

Figure 4 shows a means for supporting the top of a wall when the top anchor is placed on a bond beam in a lower course. This detail can also be used for interior partitions.

Tensioning

At the time the tendons are stressed, the masonry is considered to have its initial strength (f ‘mi). The project specification should include either the minimum f ‘mi and minimum specified compressive strength of masonry ( f ‘m), or the amount of curing required before stressing can occur.

The sequence of tensioning, whether it is accomplished by fully stressing each tendon sequentially or by stressing the tendons in stages, is a function of the design specifications. Prestressed masonry design, and therefore the structural integrity of these walls, relies on an accurate measure of the prestress in the tendons. To ensure the required level of accuracy, Specification for Masonry Structures (ref. 4) requires that the following two methods be used to evaluate the tendon prestressing force:

1. measure the tendon elongation and compare it with required elongation based on average load-elongation curves for the prestressing tendons, and either:

2a. use a calibrated dynamometer to measure the jacking force on a calibrated gage, or

2b. for prestressing tendons using bars of less than 150 ksi (1,034 MPa) tensile strength, use load-indicating washers complying with Standard Specification for Compressible-Washer-Type Direct Tension Indicators for Use with Structural Fasteners, ASTM F 959 (ref. 5). If the two values determined by methods 1 and 2 are not within 7 percent of each other, the cause of the difference must be corrected.

QUALITY ASSURANCE

Post-tensioned walls must be constructed in conformance with masonry standards applicable to conventionally reinforced masonry. In addition to these, Specification for Masonry Structures (ref. 4) requires the following for posttensioned masonry:

In the out-of-plane direction, the tolerance for the tendon placement shall be + 1/4 in. (6 mm) for masonry beams, columns, walls, and pilasters with cross-sectional dimensions less than 8 in. (203 mm). For cross-sectional dimensions greater than 8 in. (203 mm), the tolerance increases to + 3/8 in. (10 mm).
In the in-plane direction, the tolerance for tendon placement is +1in. (25 mm).
If tolerances exceed these amounts, the Architect/Engineer should evaluate the effect on the structure.

REFERENCES

Post-Tensioned Concrete Masonry Wall Design, TEK 14-
20A. Concrete Masonry & Hardscapes Association, 2002.
Standard Specification for Loadbearing Concrete Masonry
Units, ASTM C 90-01a. ASTM International, 2001.
Building Code Requirements for Masonry Structures, ACI
530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry
Standards Joint Committee, 2002.
Specification for Masonry Structures, ACI 530.1-02/ASCE
6-02/TMS 602-02. Reported by the Masonry Standards
Joint Committee, 2002.
Standard Specification for Compressible-Washer-
Type Direct Tension Indicators for Use with Structural
Fasteners, ASTM F 959-01a. ASTM International, 2001.
Standard Specification for Grout for Masonry, ASTM C
476-01. ASTM International, 2001.