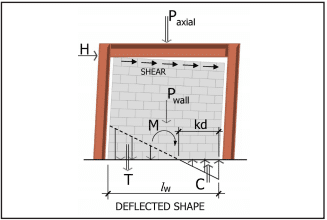
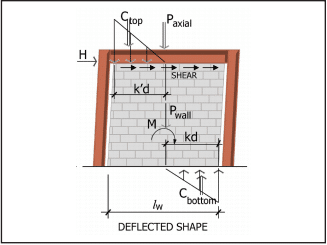
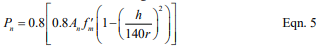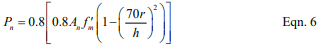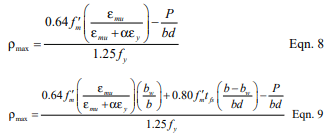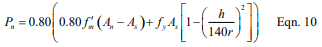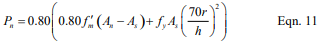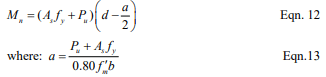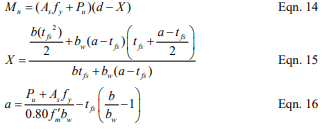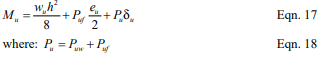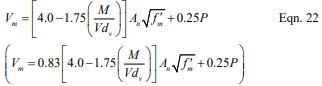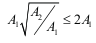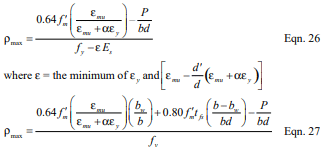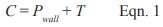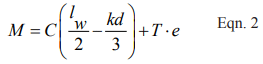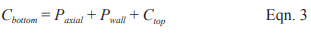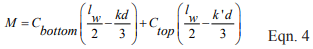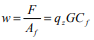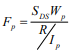Home / Technical Resources / reinforced concrete masonry

Resources

Strength Design Provisions for Concrete Masonry

August 2018

INTRODUCTION

Concrete masonry elements can be designed using one of several methods in accordance with Building Code Requirements for Masonry Structures (ref. 1): empirical design, strength design or allowable stress design. This TEK provides a basic overview of design criteria and requirements for concrete masonry structures designed using the strength design provisions contained in Chapter 3 of the 2002 edition of Building Code Requirements for Masonry Structures (also referred to as the MSJC Code) (ref. 1) as referenced and modified in Section 2108 of the 2003 International Building Code (IBC) (ref. 2). In addition, changes to the strength design method incorporated into the 2005 edition of the MSJC Code (ref. 3) through Section 2108 of the 2006 International Building Code (ref. 4) are also reviewed, as are modifications included in the 2008 MSJC Code (ref. 5).

For empirical and allowable stress design requirements, the user is referred to TEK 14-08B, Empirical Design of Concrete Masonry Walls (ref. 6), and TEK 14-07C, ASD of Concrete Masonry (2012 IBC & 2011 MSJC) (ref. 7), respectively. Tables, charts, and additional design aids specific to the design of various concrete masonry elements can be found in other related TEK.

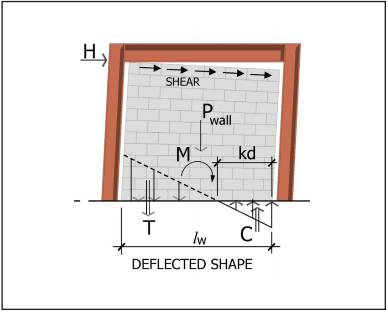
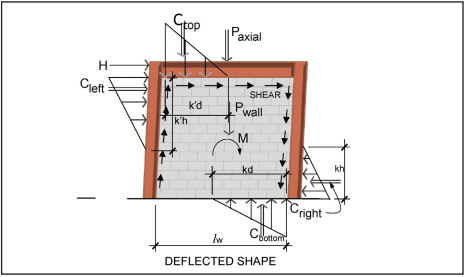
Strength design is based on the following design assumptions in conjunction with basic principles of engineering mechanics (refs. 1, 3, 5), as shown in Figure 1 for a reinforced element:

Plane sections before bending remain plane after bending. Therefore, strain in the masonry and in reinforcement, if present, is directly proportional to the distance from the neutral axis.
For unreinforced masonry, the ﬂexural stresses in the masonry are assumed to be directly proportional to strain. For reinforced masonry, the tensile strength of the masonry is neglected when calculating ﬂexural strength, but considered when calculating deﬂection.
The units, mortar, grout and reinforcement for reinforced masonry act compositely to resist applied loads.
The nominal strength of masonry cross-sections for combined ﬂexure and axial load is based on applicable conditions of equilibrium.
The maximum masonry compressive stress is 0.80f’_m for both reinforced and unreinforced masonry.
The maximum usable strain, ε_mu, at the extreme compression ﬁber of concrete masonry is 0.0025.
For reinforced masonry, compression and tension stresses in the reinforcement below the speciﬁed yield strength, f_y, are taken equal to the modulus of elasticity of the reinforcement, Es, times the steel strain ε_s. For strains greater than the yield strain corresponding to f_y, stress in the reinforcement is taken equal to f_y.
For reinforced masonry, the compressive stress is rectangular and uniformly distributed over an equivalent compression zone, bounded by the compression face of the masonry with a depth of a = 0.80c.

Based on the prescribed design model outlined above, the internal distribution of stresses and strains is illustrated in Figure 1 for a reinforced masonry element. A more comprehensive review of the design model is provided in Masonry Structures, Behavior and Design (ref. 8).

Figure 1—Stress and Strain Distribution for Strength Design of Reinforced Masonry

2003 IBC STRENGTH DESIGN MODIFICATIONS

The 2003 IBC adopts the 2002 MSJC Code with two modiﬁcations speciﬁc to the strength design procedure in IBC Section 2108. The two modiﬁcations are as follows.

Section 2108.2 introduces a maximum effective compression width for out-of-plane bending of six times the nominal wall thickness, not to exceed the reinforcement spacing. This is similar to limits historically used by the allowable stress design provisions in the MSJC Code as well as those adopted into the 2005 MSJC Code for strength design, as reviewed below.
Welded and mechanical splices incorporated into masonry elements designed by the strength design method must also comply with Section 2108.3 of the 2003 IBC. For welded splices, the reinforcement to be welded must comply with ASTM A 706 (ref. 9). Splicing by mechanical connectors is classified as either Type 1 or Type 2 mechanical splices in accordance with ACI 318, Building Code Requirements for Structural Concrete (ref. 10). Type 1 mechanical splices are only required to develop 125 percent of the nominal yield strength of the reinforcement being spliced. Type 2 mechanical splices, conversely, must develop the full specified tensile strength of the reinforcement. Welded and Type 1 mechanical splices are not permitted to be used in the plastic hinge region of intermediate or special reinforced masonry shear walls.

2002 MSJC CODE STRENGTH DESIGN CRITERIA

Using strength design, the design strength of a masonry element is compared to the required (or factored) strength (indicated by the subscript u), which includes load factors to account for the uncertainty in predicting design loads and the probability of more than one design load acting simultaneously. The required strength is based on the strength design load combinations as required by Section 1605 of the IBC. At the option of the designer, or when the MSJC Code is used in conjunction with another building code that does not contain load combinations, masonry structures are designed to resist the load combination speciﬁed in ASCE 7, Minimum Design Loads for Buildings and Other Structures (ref. 11). For strength design, these load combinations are effectively the same.

The design strength of masonry is the nominal strength (indicated by the subscript n) multiplied by an appropriate strength reduction factor, Φ. The design is acceptable when the design strength equals or exceeds the factored strength (i.e., when ΦM_n ≥ M_u) for all prescribed load combinations. The following sections cover the general strength design requirements applicable to both unreinforced and reinforced masonry assemblies, with the exception of design requirements for anchor bolts and lap splices. For these topics, the user is referred to TEK 12-03C, Design of Anchor Bolts Embedded in Concrete Masonry (ref. 12) and TEK 12-06A, Splices, Development and Standard Hooks for CM Based on the 2009 & 2012 IBC (ref. 13), respectively.

Strength Reduction Factors

To account for uncertainties in construction, material properties, calculated versus actual strengths and anticipated failure modes, the nominal strength of a masonry element is multiplied by an appropriate strength reduction factor, Φ. Strength reduction factors are used in conjunction with the load factors applied to the design loads. The values of the strength reduction factors for various types of loading conditions are:

for reinforced masonry elements subjected to ﬂexure or axial loads; Φ = 0.90;
for unreinforced masonry elements subjected to ﬂexure or axial loads; Φ = 0.60;
for masonry elements subjected to shear loads; Φ = 0.80;
for bearing on masonry elements; Φ = 0.60.

Drift and Deﬂection

When designing for earthquakes, the story drift (the relative displacement of adjacent stories) must be checked against the IBC prescribed allowable story drifts. When the MSJC Code is used in conjunction with a building code that does not contain allowable story drifts, the provisions of ASCE 7 are used. For masonry buildings with cantilevered shear walls, the IBC limits the story drift to 0.01h_sx, where h_sx is the height of the story below the level for which the drift is being calculated. For other types of masonry shear wall buildings, except masonry frames, the allowable story drift is limited to 0.007h_sx. While the IBC includes story drift limits for masonry frame wall buildings, such structural conﬁgurations are rarely used. When calculating story drift, the calculated elastic deﬂection is multiplied by the deﬂection ampliﬁcation factor, C_d, as prescribed in the IBC for the type of structural system being designed. The deﬂection ampliﬁcation factor approximates the additional deﬂection due to inelastic response (if applicable) of the system during an earthquake. Due to the inherent in-plane stiffness of masonry assemblies, in-plane deﬂection and story drift are rarely a controlling limit unless a relatively large number of openings is incorporated that reduces the strength and stiffness along a line of lateral resistance.

Unlike allowable stress design, which permits deﬂections to be calculated assuming uncracked sections for both reinforced and unreinforced masonry, strength design requires that deﬂections of reinforced masonry elements be based on cracked section properties, which are limited to one-half of the gross section properties unless a rigorous cracked section analysis is performed. The deﬂection of unreinforced masonry elements, which are required to remain uncracked, use uncracked section properties.

Because unreinforced masonry elements must be designed to remain uncracked, deﬂection is rarely a controlling design limit for these systems. Reinforced masonry elements, however, particularly tall, slender walls bending in the out-of-plane direction, may exhibit excessive deﬂection even at relatively low applied loads. As such, the MSJC Code limits the mid-height deﬂection, δ_s, of reinforced masonry elements bending in the out-of-plane direction due to service level lateral and axial loads to 0.007h. Second order effects due to P-delta contributions must also be taken into account, which is usually accomplished through iteration until convergence is achieved.

When the applied moment, M_ser, is less than the moment required to cause cracking, M_cr, (M_ser< M_cr) then the mid-height deﬂection of a masonry element subjected to a uniform out-of-plane load can be determined using Equation 1.

Conversely, when the applied moment, M_ser, is greater than the moment required to cause cracking, M_cr, but less than the nominal moment strength of the assembly (M_cr < M_ser < M_n) the mid-height deﬂection of a masonry element subjected to a uniform out-of-plane load can be determined using Equation 2.

The MSJC does not prescribe a method of determining the cracked moment of inertia, Icr. As such, any rational method of determining cracked section properties is permitted. CMUTEC-002-23, Weights and Section Properties of Concrete Masonry Assemblies (ref. 14), provides typical section properties for various uncracked wall sections. For use in Equations 1 and 2, the cracking moment can be taken as:

Where the modulus of rupture, f_r, is obtained from Table 1 for the type of mortar and construction under consideration.

Material Properties

Due to the lack of available research data substantiating its use, the speciﬁed compressive strength of concrete masonry, f’m, designed by the strength design method is required to be at least 1,500 psi (10.34 MPa), but not larger than 4,000 psi (27.58 MPa). In addition, when used in a structural role, the speciﬁed compressive strength of grout is required to be at least equal to the speciﬁed compressive strength of concrete masonry, but not greater than 5,000 psi (34.47 MPa). For each of these upper limits on masonry assembly or grout compressive strength, the actual tested strength is permitted to exceed these values: the restriction applies only to speciﬁed strengths upon which the design is based. Note that these provisions are included in the 2005 MSJC Code as well.

Strength design of reinforced masonry is based on the speciﬁed yield strength of reinforcement, f_y, which is limited to 60,000 psi (413.7 MPa). The actual yield strength of the reinforcement is limited to 1.3 times the speciﬁed yield strength. The combination of these requirements effectively precludes the use of bed joint reinforcement to be used as primary structural steel in masonry designed by the strength design method, because the nominal yield strength of bed joint reinforcement exceeds these limits. The compressive resistance of steel reinforcement is not permitted to be used unless lateral reinforcement is provided in compliance with Chapter 2 of the MSJC Code, except as permitted when checking the maximum reinforcement limits as described later.

Unreinforced Masonry

For unreinforced masonry, the masonry assembly (units, mortar and grout, if used) is designed to carry all applied stresses. The additional capacity from the inclusion of reinforcing steel, if present (such as reinforcement added to control shrinkage cracking or prescriptively required by the code), is neglected when designing unreinforced masonry elements. Because the masonry resists both tension and compression stresses resulting from applied loads, the masonry must be designed to remain uncracked.

Unreinforced Nominal Flexural Strength

The nominal ﬂexural tensile strength of unreinforced concrete masonry is given by the modulus of rupture as prescribed in the MSJC Code, which varies with the direction of span, mortar type, bond pattern and percentage of grouting as shown in Table 1. These values apply to masonry subject to out-of-plane bending. For walls spanning horizontally between supports, the code conservatively assumes that stack bond masonry has no ﬂexural bond strength across the mortared head joints, thus only the grout area (for horizontally grouted sections) is used. For this case, the modulus of rupture of the grout is taken equal to 250 psi (1720 kPa). Likewise, for masonry subjected to in-plane bending, the modulus of rupture normal and parallel to the bed joints is taken as 250 psi (1720 kPa).

For masonry elements subjected to a factored bending moment, M_u, and a compressive axial force, P_u, the resulting ﬂexural bending stress is determined using Equation 4.

If the resulting value of F_u is positive, then the masonry section is controlled by tension and the modulus of rupture values of Table 1, reduced by the appropriate strength reduction factor (Φ = 0.60), must be satisﬁed. Conversely, if F_u as given by Equation 4 is negative, the masonry section is in compression and the design compressive stress of 0.80f’m applies. When using axial load to offset ﬂexural bending stresses as described above, only dead loads or other permanent loads should be included in P_u.

Unreinforced Nominal Axial Strength

When unreinforced masonry walls are subjected to compressive axial loads only, the nominal axial compressive strength, P_n, is determined using equation 5 or 6, as appropriate. Unreinforced masonry is not permitted to carry net axial tension forces.

For elements with h/r not greater than 99:

For elements with h/r greater than 99:

Unreinforced Nominal Shear Strength

Shear stresses on unreinforced masonry elements are calculated using the net cross-sectional properties of the masonry in the direction of the applied shear force using:

Equation 7 is applicable to determining both in-plane and out-of-plane shear stresses. Because unreinforced masonry is designed to remain uncracked, it is not necessary to perform a cracked section analysis to determine the net section properties. In turn, the applied shear stresses (factored accordingly for the appropriate load combination) are compared to the nominal shear strength, V_n, of an unreinforced masonry section, which is the least of:

Table 1—Modulus of Rupture Values, psi (kPa)

Reinforced Masonry

The design of reinforced masonry in accordance with the MSJC Code neglects the tensile resistance provided by the masonry units, mortar and grout in determining the strength of the masonry assemblage. (The tensile strength of the units, mortar, and grout is considered, however, in determining the stiffness and deﬂection of a reinforced masonry element.) Thus, for design purposes, the portion of masonry subject to net tensile stress is assumed to have cracked, transferring all tensile forces to the reinforcement.

Using strength design, reinforcing bars used in masonry may not be larger than No. 9 (M #29) and bars may not be bundled. Further, the nominal bar diameter is not permitted to exceed one-eighth of the nominal member thickness or one-quarter of the least clear dimension of the cell, course or collar joint in which it is placed. The total area of reinforcing bars placed in a single cell or in a course of hollow unit construction may not exceed 4% of the cell area. Note that this limit does not apply at sections where lap splices occur. At lap splices, the maximum reinforcing bar area is increased to 8%, in both the 2002 and 2005 editions of the MSJC Code.

Maximum Flexural Reinforcement Ratio

To provide for a prescribed level of reinforced masonry ductility in the event of failure, the maximum reinforcement ratio, ρ_max, is limited in accordance with Equation 8 or 9, as appropriate. Equation 8 applies to masonry cross sections that are fully grouted or where the neutral axis falls within the face shell of the masonry units in partially grouted construction. When the neutral axis falls within the cores of partially grouted construction, Equation 9 is used.

The tension reinforcement yield strain factor, α, varies with the seismic response modiﬁ cation factor, R, masonry element, and type of loading as follows:

α = 1.3 for walls subjected to out-of-plane forces and designed using an R value greater than 1.5,
α = 5.0 for walls subjected to in-plane forces, for columns and for beams designed using an R > 1.5,
α = 2.0 for masonry structures designed using an R ≤ 1.5.

In the above set of requirements, R is larger for out-of-plane loads when R is less than or equal to 1.5, which is contrary to the underlying intent of providing increased ductility for systems and elements whose ductility demand may be relatively high. Several updates and revisions to the maximum have been incorporated into subsequent editions to the 2002 MSJC Code as reviewed below.

Reinforced Nominal Axial Strength

The nominal axial strength, P_u, of masonry walls, piers and columns, modiﬁed to account for the effects of slenderness, is determined using equation 10 or 11, as appropriate. The MSJC Code also limits the factored axial stress to 0.20f’m.

For elements with h/r not greater than 99:

For elements with h/r greater than 99:

Note that the reinforcing steel area, A_s, is included in the nominal axial strength calculation only if it is laterally conﬁned in accordance with Chapter 2 of the MSJC Code.

Reinforced Nominal Flexural Strength

The nominal ﬂexural strength, M_n, of a reinforced masonry element is determined as outlined below. In addition, the nominal ﬂexural strength at any section along a member must be at least one-fourth of the maximum nominal ﬂexural strength at the critical section.

When there are no axial loads, or when axial loads are conservatively neglected as may be appropriate in some cases, there are several circumstances to consider when determining the nominal ﬂexural strength of reinforced masonry walls. For a fully grouted element, the internal moment arm between the resulting compressive and tensile forces is resolved to determine the resisting capacity of the section. Partially grouted walls are analyzed in the same way, but with the additional consideration of the possible inﬂuence of the ungrouted cores on the strength of the section. For partially grouted masonry bending out-of-plane, there are two types of behavior to consider.

In the ﬁrst case, when the neutral axis (the location of zero stress) lies within the compression face shell, the wall is analyzed and designed using the procedures for a fully grouted wall.
In the second case, when the neutral axis lies within the core area, the portion of the ungrouted cells must be deducted from the area of masonry capable of carrying compression stresses.

The neutral axis location depends on the reinforcement spacing as well as the reinforcement ratio, ρ, and the distance between the reinforcement and the extreme compression ﬁber, d.

When analyzing partially grouted walls, it is typically initially assumed that the neutral axis lies within the compression face shell, as the analysis is more straightforward. The value of c is then calculated based on this assumption. If it is determined that the neutral axis lies outside the compression face shell, the more rigorous tee beam analysis is performed. Otherwise, the rectangular beam analysis is carried out.

Rectangular Beam Analysis

For fully grouted masonry elements and for partially grouted masonry walls with the neutral axis in the compression face shell, the nominal ﬂexural strength, M_n, is calculated using equations 12 and 13 as follows:

Tee Beam Analysis

For partially grouted masonry walls where the neutral axis is located within the cores, the nominal ﬂexural strength, M_n, is calculated using equations 14, 15, and 16 as follows:

To account for deﬂection resulting from out-of-plane loads and the additional bending moment due to eccentrically applied axial loads, the factored bending moment at the mid-height of a simply supported wall under uniform loading is required to be determined by Equation 17.

Multiple iterations may be necessary to determine the converging value of the resulting deﬂection.

Reinforced Nominal Shear Strength

Shear acting on reinforced masonry members is resisted by the masonry and shear reinforcement, if provided, in accordance with the following:

Where V_n may not exceed the values given by Equations 20 or 21, as appropriate.

Where M/Vd_v is less than or equal to 0.25:

Where M/Vd_v is greater than 1.00:

For values of M/Vd_v between 0.25 and 1.00, the maximum value of V_n may be linearly interpolated.

The nominal shear strength provided by the masonry is determined in accordance with the following.

Where the value of M/Vd_v need not be taken greater than 1.0.

When shear reinforcement is incorporated into reinforced masonry construction, the shear strength provided by the reinforcement is calculated in accordance with the following.

2006 IBC REQUIREMENTS

The following is a brief summary of the changes and modiﬁcations adopted into the 2005 MSJC Code as referenced in the 2006 IBC. The majority of the basic design provisions remain unchanged, with several notable exceptions as reviewed below.

2006 IBC Strength Design Modiﬁcations

The same modiﬁcations for welded and mechanical splices previously discussed in the 2003 IBC Strength Design Modiﬁcations section remain in the 2006 IBC. In addition, Section 2108 of the 2006 IBC has incorporated a limit of 72d_b on the maximum required length of lap splices used in masonry designed by the strength design method as determined by the 2005 MSJC lap splice provisions. While this limit is typically not triggered for relatively small bar diameters, it can reduce the required lap length of large diameter reinforcing bars or in cases where small cover distances are used. Refer to TEK 12-06A (ref. 13) for detailed splice length requirements.

Other changes to Section 2108 of the 2006 IBC reﬂect updates and modiﬁcations to the 2005 MSJC Code to remove redundant or conﬂicting requirements.

2005 MSJC Code Strength Design Criteria Bearing Strength

Due primarily to oversight, the 2002 MSJC Code did not include explicit provisions for determining the bearing strength of masonry subjected to concentrated loads. The bearing strength requirements adopted into the 2005 MSJC Code are similar to those used for allowable stress design, modiﬁed as necessary for use in strength design. The nominal bearing strength of masonry is taken as the greater of Equations 24 and 25:

The value of 0.6 in Equations 24 and 25 is a design coefﬁcient, not the strength reduction factor, Φ, which also happens to be equal to 0.6 for determining the design bearing strength. For use in Equation 25, the following expression must also be satisﬁed:

Where A₁ is the actual bearing area directly under the bearing plate and A₂ is the effective bearing area, deﬁned as a right o pyramid having A₁ as a top plane and sloping at 45 . For walls laid in stack bond, the area deﬁned by A₂ is terminated at head joints unless a bond beam or other means of distributing stresses is used. The concentrated stresses are distributed over a length equal to the width of the bearing area plus four times the thickness of the supporting element, but not to exceed the center-to-center distance between the concentrated loads.

Modulus of Rupture

The 2005 MSJC Code incorporated a few modiﬁcations to the modulus of rupture values presented in Table 1 for ﬂexural tension stresses normal to the bed joints of hollow, fully grouted assemblies, as shown in Table 2. These modiﬁcations recognize that the type of mortar has less of an inﬂuence on the modulus of rupture when the element is fully grouted.

In addition, instead of prescribing a single value of 250 psi (1.72 MPa) for masonry subjected to in-plane bending as in the 2002 MSJC Code, the 2005 MSJC Code requires the use of Table 1, as modiﬁed by Table 2, for all cases of in-plane and out-of-plane bending.

Table 2—Modiﬁ cations to Modulus of Rupture Values in Table 1, as Included in the 2005 MSJC Code, psi (kPa)

Maximum Flexural Reinforcement Limits

The maximum ﬂexural reinforcement requirements in the 2005 MSJC employ the same strain gradient approach as reviewed above, with several notable revisions.

Reinforcement is permitted to carry compression stresses, with or without lateral conﬁning reinforcement. Further, the 1.25 factor on the nominal yield stress of the reinforcement as been removed. The resulting equations for the maximum ﬂexural reinforcement limits are given by Equation 26 for fully grouted members or members subjected to in-plane loads, and Equation 27 for partially grouted masonry assemblies subjected to out-of-plane loads where the neutral axis falls in an open cell.

The tension reinforcement yield strain factor, α, is taken equal to the following values when M_u/V_ud_v ≥ 1.0 (indicating performance is dominated by ﬂexure):
- for intermediate reinforced masonry shear walls subjected to in-plane loads: α = 3.0,
- for special reinforced masonry shear walls subjected to in-plane loads: α = 4.0,
- for other masonry elements and loading conditions: α= 1.5.
For cases where M_u/V_ud_v ≤ 1.0 (indicating shear dominated performance) and R > 1.5: α = 1.5.
For masonry members where M_u/V_ud_v ≤ 1.0 and R ≤ 1.5, there is no limit on the amount of reinforcement permitted.
The axial load, P, for use in Equations 26 and 27, is the gravity axial load component determined from the following load combination: D + 0.75L + 0.525Q_E.

Effective Compression Width per Reinforcing Bar

Section 2108 of the 2003 IBC included limits on the effective compression width per reinforcing bar, which were subsequently removed from the 2006 IBC, as similar provisions were incorporated into the 2005 MSJC Code. For masonry construction in running bond, and for masonry in stack bond construction with bond beams space no further than 48 in. (1,219 mm) on center, the maximum width of the compression area used is limited to the least of:

the center-to-center spacing of the reinforcement;
six times the nominal thickness of the element; or
72 in. (1,829 mm).

Boundary Elements

New to the 2005 MSJC Code are design provisions for boundary elements incorporated into the end zones of masonry shear walls. Because the MSJC does not include minimum prescriptive reinforcement detailing requirements for boundary elements, it requires that when used, their performance be veriﬁed by testing. In addition, when meeting the requirements for geometrical symmetry, axial load and ﬂexural performance, the MSJC Code permits the maximum reinforcement limits as reviewed above to be waived. This exception may or may not require the incorporation of special boundary elements, depending on the design circumstances.

2008 MSJC STRENGTH DESIGN REQUIREMENTS

At the time of publication, the 2008 edition of the MSJC Code had been ﬁnalized, but the 2009 edition of the IBC had not. In anticipation of the 2009 IBC adopting the 2008 MSJC by reference, following is a brief overview of changes to the strength design provisions of the 2008 MSJC Code. In addition to some reorganization, substantive revisions to the strength design method include:

The shear strength check to help preclude brittle failure of a masonry element during an earthquake was revised to apply only to special reinforced masonry shear walls. Previously, this check applied to both reinforced and unreinforced masonry elements regardless of seismic considerations.
The requirement to provide at least 80 percent of the lateral stiffness through shear walls was revised to apply only to Seismic Design Categories C and higher.
Instead of requiring that the deﬂection of all reinforced masonry elements be calculated on cracked section properties, the 2008 MSJC Code simply requires that the design “consider the effects of cracking and reinforcement on member stiffness,” thereby permitting more ﬂexibility in design application.
A moment magniﬁer approach was incorporated for unreinforced masonry design in determining the inﬂuence of P-delta effects. The magniﬁed moment, M_c, is determined either through a second-order analysis, or by the following:

For members with h/r ≤ 45, it is permitted to take δ = 1.0. For members with 45 < h/r ≤ 60, it is permitted to take δ = 1.0 provided that the maximum factored axial stress on the element does not exceed 0.72f’m.

NOTATIONS

A_n = net cross-sectional area of masonry, in.² (mm²)
A_s = effective cross-sectional area of reinforcement, in.² (mm²)
A_v = cross-sectional area of shear reinforcement, in.² (mm²)
A₁ = bearing area under bearing plate, in.² (mm²)
A₂ = effective bearing area, in.² (mm²)
a = depth of an equivalent compression zone at nominal strength, in. (mm)
b = width of section, in. (mm)
b_w = for partially grouted walls, width of grouted cell plus each web thickness within the compression zone, in. (mm)
C = resultant compressive force, lb (N)
c = distance from the ﬁber of maximum compressive strain to the neutral axis, in. (mm)
C_d = seismic deﬂection ampliﬁcation factor
C_n = nominal bearing strength, lb (N)
D = dead load, lb (N)
d = distance from the extreme compression ﬁber to centroid of tension reinforcement, in. (mm)
d_b = nominal diameter of reinforcement, in. (mm)
d_v = actual depth of masonry in direction of shear considered, in. (mm)
d’ = distance from the extreme tension ﬁber to centroid of compression reinforcement, in. (mm)
E_m = modulus of elasticity of masonry, psi (MPa)
E_s = modulus of elasticity of reinforcement, psi (MPa)
e_u = eccentricity of P_uf in. (mm)
F_u = net ﬂexural bending stress due to factored loads, psi (MPa)
F_vu = shear stress on unreinforced masonry elements, psi (MPa)
f’_m = specified compressive strength of masonry, psi (MPa)
f_r = modulus of rupture, psi (MPa)
f_y = speciﬁed yield strength of reinforcement, psi (MPa)
h = effective height of masonry element, in. (mm)
h_sx = effective height of masonry element below level x, in. (mm)
I_cr = moment of inertia of cracked cross-sectional area of a member, in.⁴ (mm⁴)
I_g = moment of inertia of gross cross-sectional area of a member, in.⁴ (mm⁴)
I_n = moment of inertia of net cross-sectional area of a member, in.⁴ (mm⁴)
L = live load, lb (N)
M = unfactored maximum calculated bending moment at the section under consideration, in.-lb (N-mm)
M_c = factored moment magniﬁed for the effects of member curvature, in.-lb (N-mm)
M_cr = cracking bending moment, in.-lb (N-mm)
M_n = nominal moment strength, in.-lb (N-mm)
M_ser = applied bending moment, in.-lb (N-mm)
M_u = factored moment, in.-lb (N-mm)
N_v = compressive force acting normal to the shear surface, lb (N)
P = unfactored axial load, lb (N)
P_n = nominal axial strength, lb (N)
P_u = factored axial load, lb (N)
P_uf = factored load from tributary ﬂoor or roof areas, lb (N)
P_uw = factored weight of wall area tributary to wall section under consideration, lb (N)
Q_E = the effect of horizontal seismic forces, lb (N)
Q_n = ﬁrst moment about the neutral axis of a section of that portion of the net cross section lying between the neutral axis and extreme ﬁber, in.³ (mm³)
R = seismic response modiﬁcation factor
r = radius of gyration, in. (mm)
S_n = section modulus of cross-section, in.³ (mm³)
s = spacing of shear reinforcement, in. (mm)
T = tension in reinforcement, lb (N)
t = speciﬁed thickness of masonry element, in. (mm)
t_fs = concrete masonry face shell thickness, in. (mm)
V = unfactored shear force, lb (N)
V_m = shear strength provided by masonry, lb (N)
V_n = nominal shear strength, lb (N)
V_s = shear strength provided by shear reinforcement, lb (N)
V_u = factored shear, lb (N)
w_u = out-of-plane factored uniformly distributed load, lb/in. (N/mm)
X = for partially grouted masonry, distance from extreme compression ﬁber to centroid of the compression resultant, in. (mm)
α = tension reinforcement yield strain factor
δ = moment magniﬁcation factor
δ_s = deﬂection due to service loads, in. (mm)
δ_u = deﬂection due to factored loads, in. (mm)
ε_mu = maximum usable compressive strain of masonry
ε_s = steel strain
ε_y = yield strain of reinforcement
ρ = reinforcement ratio
ρ_max = maximum reinforcement ratio
Φ = strength reduction factor

REFERENCES

Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
2003 International Building Code. International Code Council, 2003.
Building Code Requirements for Masonry Structures, ACI 530-05/ASCE 5-05/TMS 402-05. Reported by the Masonry Standards Joint Committee, 2005.
2006 International Building Code. International Code Council, 2006.
Building Code Requirements for Masonry Structures, ACI 530-08/ASCE 5-08/TMS 402-08. Reported by the Masonry Standards Joint Committee, 2008.
Empirical Design of Concrete Masonry Walls, TEK 1408B, Concrete Masonry & Hardscapes Association, 2008.
ASD of Concrete Masonry (2012 IBC & 2011 MSJC), TEK 14-07C, Concrete Masonry & Hardscapes Association, 2004.
Drysdale, R. G., Hamid, A. A. and Baker L. R., Masonry Structures, Behavior and Design, Second Edition. The Masonry Society, 1999.
Standard Speciﬁcation for Low-Alloy Steel Deformed and Plain Bars for Concrete Reinforcement, ASTM A 706/A 706M-01. ASTM International, 2001.
Building Code Requirements for Structural Concrete, ACI 318-02. American Concrete Institute, 2002.
Minimum Design Loads for Buildings and Other Structures, ASCE 7-02. Structural Engineering Institute of the American Society of Civil Engineers, 2002.
Design of Anchor Bolts Embedded in Concrete Masonry, TEK 12-03C. Concrete Masonry & Hardscapes Association, 2013.
Splices, Development and Standard Hooks for CM Based on the 2009 & 2012 IBC, TEK 12-06A, Concrete Masonry & Hardscapes Association, 2013.
Weights and Section Properties of Concrete Masonry Assemblies, CMU-TEC-002-23, Concrete Masonry & Hardscapes Association, 2023.

Hybrid Concrete Masonry Design

August 2018

INTRODUCTION

Hybrid masonry is a structural system that utilizes reinforced masonry infill walls with a framed structure. While the frame can be constructed of reinforced concrete or structural steel, the discussion here will include steel frames in combination with reinforced concrete masonry walls. The masonry walls are used as part of the lateral load resisting system.

Following the development of the wrought iron framed Glass Palace in France in 1851, framed technology evolved and spread to the United States. Since then, combining masonry walls with frames has been used as a common feature of many early building types.

Caged construction was introduced in 1882 by architect George Post. The first caged framed building used a structural steel framework mixed with exterior walls of unreinforced masonry. The term caged walls resulted from the exterior walls being built around a structural cage. The frame supported the floor and roof gravity loads; the masonry was independent of the frame and self-supporting and provided the lateral stiffness. As a result, the wall thicknesses were only slightly less than those in bearing wall buildings.

Another type of structure used exterior unreinforced bearing walls and interior structural frames. The famous Monadnock Building in Chicago, constructed in 1892 is an example of this type with exterior masonry bearing walls up to 6 ft (1.83 m) thick. The 15-story building was the largest office building in the world when completed. Ironically, it was the last high-rise built with exterior masonry bearing walls for the full height of the building and an interior frame.

Transitional buildings were perhaps the most used type of combination frame/masonry structures used through the 1940s. An example is the 13-story Tower Building in New York built in 1888, which used transitional and load bearing construction. Transitional buildings took traditional masonry walls and constructed them integrally with the exterior structural frame. Brick or hollow clay tile was used as an inner wythe, usually 8 in. (203 mm) thick. An exterior wythe of brick, cast stone, terra-cotta or stone was anchored or headered to the backup to function as a composite wall system, but there was no accommodation for the masonry walls to take differential movement. It was common to design these buildings for gravity loads only. While the wall system was not intended to be structural, it provided lateral stiffness. The masonry also provided exterior finish, fire protection for the frame, and backup for the interior finish.

Confined masonry within concrete frames is yet another form of combination structure. This system originated in the 1800s. It has developed globally but apparently has no specific origin. Confined masonry is used primarily for residential construction. The type of masonry infill varies by region or country and includes clay brick, clay tile, stone or concrete masonry.

As framed structures grew taller, architects tried to reduce the thickness of the exterior walls. The structural steel and reinforced concrete structures were used to support building loads and exterior wall loads. Curtain walls and cavity walls developed during this time and masonry was no longer the only wall material used as a backup system for exterior walls.

The concept of using masonry infill to resist lateral forces is not new; having been used successfully throughout the world in different forms. While common worldwide, U.S. based codes and standards have lagged behind in the establishment of standardized means of designing masonry infill.

The hybrid masonry system outlined in this TEK is a unique method of utilizing masonry infill to resist lateral forces. The novelty of the hybrid masonry design approach relative to other more established infill design procedures is in the connection detailing between the masonry and the steel frame, which offers multiple alternative means of transferring loads into the masonry—or isolating the masonry infill from the frame.

Prior to implementing the design procedures outlined in this TEK, users are strongly urged to become familiar with the hybrid masonry concept, its modeling assumptions, and its limitations particularly in the way in which inelastic loads are distributed during earthquakes throughout the masonry and frame system. This system, or design methods, should not be used in Seismic Design Category D and above until further studies and tests have been performed; and additional design guidance is outlined in adopted codes and standards.

HYBRID MASONRY CONCEPT

Since the 1950s, architects and engineers have primarily used cavity walls with framed structures. The backup masonry walls are generally termed infill walls. They support out-of-plane loads on the wall and are isolated from the frame so as not to participate in the lateral load resistance (see Figure 1). Codes usually require that these walls be isolated from the lateral movement of the frame to ensure that lateral loads are not imparted to the masonry.

The hybrid system is a variation of the confined masonry system. It incorporates the beneficial qualities of transitional buildings and the characteristics of cavity wall construction. It differs from cavity wall construction in that the infill masonry walls participate with the frame and provide strength and stiffness to the system. The masonry can be used as single wythe or as cavity wall construction. Hybrid masonry structures are constructed of reinforced masonry, not unreinforced masonry, as was common in transitional buildings.

Hybrid masonry/framed structures were first proposed in print in 2006 (ref. 1). There are several primary reasons for its development. One reason is to simplify the construction of framed buildings with masonry infill. While many designers prefer masonry infill walls as the backup for veneers in framed buildings, there is often a conflict created when steel bracing is required and positioned such that conflicts arise with the masonry infill. This leads to detailing difficulties and construction interferences in trying to fit masonry around the braces. One solution is to eliminate the steel bracing and use reinforced masonry infill as shear wall and bracing.

Hybrid masonry/steel structures also provide structural redundancy that can be utilized to limit progressive collapse. The reinforced masonry infill provides an alternative load path for the frame’s gravity loads, hence providing redundancy. The resulting system is more efficient than either a frame or a bearing wall system alone when subjected to progressive collapse design conditions. If a steel column is damaged in a hybrid structure, gravity loads will transfer to the reinforced masonry. If the masonry is damaged, the gravity load transfers to the frame. There are documented examples from the World Trade Center disaster that illustrate redundancy in transitional buildings (ref. 2).

CLASSIFICATION OF WALLS

There are three hybrid wall types. The loadings these walls can support is dependent upon the degree of confinement of the masonry within the frame. These walls can potentially transfer axial loads from the beam/girder of the frame as well as transfer shear from the beam/girder or the columns. The wall systems are defined in Table 1 based on their ability to transfer loads from the frame to the wall. All wall systems listed can address the backup for cavity wall construction. If a veneer is used, it is constructed with relieving angles and is isolated for differential movement as with conventional cavity wall construction. By comparison, an infill wall used in a cavity wall does not transfer axial load or in-plane shear.

The following sections describe each wall type. The key to the performance of the walls is the confinement at the columns and the top of the wall along with the anchorage.

Type I Hybrid Walls

This wall type transmits out-of-plane loads and in-plane shear loads (Figure 1). The gap at the top and the top anchors should not transmit axial loads. If column anchors are used, they should not transmit shear loads. The gaps at the columns must be adequate so the columns do not bear against the masonry when the frame undergoes drift.

All wall types must transfer shear at the base of the wall. This is commonly done using dowels into the foundation or on the framing at the bottom of the wall.

The tie-down forces are a key component to the support of the wall against preventing overturning.

Effectively, the masonry wall is a nonloadbearing shear wall that also supports out-of-plane loads. The in-plane forces are shown in Figure 2. These forces must be applied to the frame design. The tension load T can be accommodated by the distributed reinforcement or the designated tie-down reinforcement. This same reinforcement can be used to distribute shear forces as well. Type I walls can be ideal for buildings up to four stories.

The forces are resolved into:

where e is the eccentricity of the tie-down force, which is defined as the distance between the tie-down reinforcement and the center of the wall.

Type II Hybrid Walls

The Type II hybrid wall is a modification of Type I. It is constructed tight to the beam framing above such that axial loads are transmitted to the masonry wall (Figure 3). The top anchors transmit out-of-plane loads and shear loads. If column anchors are used, they do not transmit shear loads.

Effectively, the masonry wall is a loadbearing shear wall that also supports out-of-plane loads.

There are two options for distributing the in-plane forces resulting from overturning of the shear wall, designated Type IIa and Type IIb. For Type IIa (Figure 4), the tension load T can be accommodated by the distributed reinforcement or the designated tie-down reinforcement. For Type IIb (Figure 5), the tension force that tied down the wall in the Type IIa wall is replaced by compression on the upper framing and is transferred into the steel frame. This is a significant benefit in multi-story buildings because the tie-down to the frame is not required.

As previously noted, shear dowels are needed at the base of the walls. Type IIb walls, unlike Type I and IIa, do not require tension lap splices for the vertical reinforcement at the base of the walls since only shear loads are being developed.

Type II walls are generally limited to buildings 10 to 14 stories high since masonry stresses will usually govern. Generally, this limitation is similar for loadbearing buildings as well.

The designer has the option to load-share the gravity loads with the masonry wall. This can reduce the size of the beam/girder framing member. For example, if the masonry is constructed after the dead loads of the floor/roof framing system are installed, the masonry wall can take the gravity loads that are added to the structure after the walls are built. The framing (columns and beams/girders) sizes can be limited to support only the dead loads and the lateral load effects. The framing should be designed for the full gravity loads if there is a chance that the wall will be modified in the future.

For the Type IIb wall at the base of the wall:

The overturning is resolved by:

The axial load imparted to the wall is a function of the construction sequence. This should be stated in the construction documents. For example, if the steel is designed for only the slab and framing dead load and the lateral load effects, the masonry walls must be constructed tight to the framing above after the slab is in place but before the wall above is started.

The steel framing and the masonry must be designed using similar assumptions.

Type III Hybrid Walls

This wall type is fully confined within the framing (Figure 6). It is most similar to the transitional buildings from the early 1900s. However, in this modernized version the masonry is engineered and reinforced to support axial and shear loads in addition to the out-of-plane loads. As with the Type II hybrid wall, the designer has the option to design the columns and beams/girders for the portion of the gravity loads installed before the masonry.

Currently, there are no standards in the United States that govern the design of this type of wall. Research is underway to help define the behavior of these walls, which will lead to code requirements. Designers should only use this system at their own discretion. Statics can be used to generate formulas comparable to Equations 1 through 4 for Type I and II hybrid.

Figures 7 and 8 show the two variations (Type IIIa and Type IIIb) based on how the overturning force is handled.

HYBRID DESIGN

As discussed, the masonry in hybrid structures can carry out-of-plane loads in addition to in-plane loads. The masonry design can be performed based on the code for reinforced masonry using allowable stress (based on linear elastic methods). As strength design procedures gain acceptance, load factor design with non-linear elastic evaluation of the masonry will be possible.

While there are three hybrid types that dictate the loadings (Type I, II and III), there are three shear wall types available for the design of the walls themselves. The shear wall type depends on the minimum prescriptive reinforcement and grouting. The Building Code Requirements for Masonry Structures and the International Building Code (IBC) (refs. 3, 4) classify shear walls as ordinary reinforced, intermediate reinforced, or special reinforced. Therefore, there are three combinations of hybrid types to choose from.

The structural steel system design and the in-plane loads to the masonry are based upon the IBC and ASCE 7 (ref. 11) using seismic factors for R (response modification coefficient), Ω_o (system over-strength factor), and C_d (deflection amplification factor) applicable to the type of shear walls used with building frames. These factors are given in Table 2. An on-going research project at the University of Illinois is evaluating these factors for their applicability to hybrid walls.

Ordinary reinforced shear walls are permitted in Seismic Design Categories (SDCs) A, B and C. The building height is unlimited for SDCs A and B and limited to 160 ft (48.76 m) for SDC C.

Intermediate reinforced shear walls are permitted in SDCs A, B and C. The building height is unlimited.

Special reinforced shear walls are permitted in all seismic design categories. The building height is unlimited in SDCs A, B and C, limited to 160 ft (48.8 m) in SDCs D and E, and limited to 100 ft (30.5 m) in SDC F.

While these are the permitted types and classes, most projects thus far have been in SDC A, B and C. This has been convenient in that an R = 3 type structural steel design has been used in accordance with AISC. Designs in SDC D and higher would require use of the AISC Seismic Design Manual, AISC 327-05 (ref. 9). In addition, research is on-going for various aspects of the systems in higher seismic classes.

More detailed information on prescriptive seismic detailing for concrete masonry shear walls can be found in TEK 14-18A, Prescriptive Seismic Reinforcement Requirements for Masonry Structures (ref. 10).

Table 2—Factors Based On Shear Wall Type

COMPUTER SOFTWARE

Several commercial software companies have masonry design packages (refs. 5, 6), some of which have included hybrid masonry in their packages. This allows the masonry and steel to be modeled and designed as a system. The software is primarily based on allowable stress design and linear elastic analysis. There are plans to incorporate strength design in the future.

CONCLUSIONS

Hybrid masonry offers many benefits and complements framed construction. By using the masonry as a structural element for in-plane loads, the constructability of the masonry with the frames is improved, the lateral stiffness is increased, the redundancy is improved, and opportunities for reduced construction costs are created.

Designs indicate that greater stiffness can be achieved with hybrid masonry systems in comparison with braced frames or moment frames. The beneficial effect on the framing through the load-sharing abilities of the system is also evident. These qualities, stiffness, and redundancy can be useful in preventing progressive collapse.

For now, Type I and Type II hybrid systems can be designed in the United States using existing codes and standards. Criteria for Type III hybrid systems are under development.

Details for the construction of hybrid walls and design issues related to the top connectors are discussed in TEK 03-03B and IMI Technology Brief 02.13.02 (refs. 7, 8).

NOTATIONS:

C = resultant compressive force, lb (N)
C_bottom = resultant compressive force at bottom of masonry wall, lb (N)
C_d = deflection amplification factor
C_left = resultant compressive force on left side of masonry wall, lb (N)
C_right = resultant compressive force on right side of masonry wall, lb (N)
C_top = resultant compressive force at top of masonry wall, lb (N)
d = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
e = eccentricity of the tie-down force, equal to the distance of the tie-down reinforcement from the center of the wall, in. (mm)
H = shear force, lb (N)
h = effective height of masonry element, in. (mm)
k, k’ = ratio of distance between compression face of wall and neutral axis to the effective depth, d for the bottom and top of the wall; and to the height of the wall, h, for the sides, respectively.
l_w = length of entire wall or of segment of wall considered in the direction of shear force, in. (mm)
M = maximum moment at the section under consideration, in.-lb (N-mm)
P_axial = axial load, lb (N)
P_wall = axial load due to wall weight, lb (N)
R = seismic response modification factor
T = tension in reinforcement, lb (N)
Ω_o = system over-strength factor

REFERENCES

Biggs, D.T., Hybrid Masonry Structures, Proceedings of the Tenth North American Masonry Conference, The Masonry Society, June 2007.
Biggs, D.T., Masonry Aspects of the World Trade Center Disaster, The Masonry Society, 2004.
Building Code Requirements for Masonry Structures, ACI 530-08/ASCE 5-08/TMS 402-08. The Masonry Society, 2008.
2006 International Building Code. International Code Council, 2006.
RAM Advanse Version 10.0, Masonry Wall, RAM International, 2009.
RISA 3D Version 8.0, RISA Technologies.
Hybrid Masonry Construction With Structural Steel Frames, TEK 03-03B. Concrete Masonry & Hardscapes Association, 2009.
Hybrid Masonry Construction, IMI Technology Brief 02.13.02. International Masonry Institute, 2009.
AISC Seismic Design Manual, AISC 327-05. American Iron and Steel Institute, 2005.
Prescriptive Seismic Reinforcement Requirements for Masonry Structures, TEK 14-18A. Concrete Masonry & Hardscapes Association, 2003.
Minimum Design Loads for Buildings and Other Structures, ASCE 7-05. American Society of Civil Engineers, 2005.

Strength Design of Concrete Masonry Walls for Axial Load & Bending

August 2018

INTRODUCTION

Building structural design requires a variety of structural loads to be accounted for: dead and live loads, those from wind, earthquake, lateral soil pressure, lateral fluid pressure as well as forces induced by temperature changes, creep, shrinkage and differential movements. Because any load can act simultaneously with another, the designer must consider how these various loads interact on the wall. For example, an axial load can offset tension due to lateral load, thereby increasing flexural capacity, and, if acting eccentrically, can also increase the moment on the wall. Building codes dictate which load combinations must be considered, and require that the structure be designed to resist the most severe load combination.

The design aids in this TEK cover combined axial compression or axial tension and flexure, as determined using the strength design provisions of Building Code Requirements for Masonry Structures (ref. 3). For concrete masonry walls, these design provisions are outlined in Strength Design of Concrete Masonry (ref. 1). Axial load-bending moment interaction diagrams account for the interaction between moment and axial load on the design capacity of a wall. This TEK shows the portion of the interaction diagram that applies to the majority of wall designs. Although negative moments are not shown, the figures may be used for these conditions, since with reinforcement in the center of the wall wall strength will be the same under either a positive or negative moment of the same magnitude. Conditions outside of this area may be determined using Concrete Masonry Wall Design Software or Concrete Masonry Design Tables (refs. 4, 5). The reader is referred to Loadbearing Concrete Masonry Wall Design (ref. 2) for a full discussion of interaction diagrams.

Figures 1 through 8 apply to fully or partially grouted reinforced concrete masonry walls with a specified compressive strength f’_m of 1,500 psi (10.34 MPa), and a maximum wall height of 20 ft (6.10 m), Grade 60 (414 MPa) vertical reinforcement, with reinforcing bars positioned in the center of the wall and reinforcing bar spacing s from 8 in. to 120 in. ( 203 to 3,048 mm). Figures 1 through 8 apply to fully or partially grouted reinforced concrete masonry walls with a specified compressive strength, f’m, of 1500 psi (10.34 MPa), and a maximum wall height of 20 ft (6.09 m), Grade 60 vertical reinforcement, with reinforcing bars positioned in the center of the wall and reinforcing bar spacing, s, from 8 in. to 120 in. ( 203 to 3,048 mm). Each figure applies to one specific wall thickness and one reinforcing bar size. For walls less than 20 ft (6.1 m) high, figures 1 through 8 will be slightly conservative due to PΔ effects.

DESIGN EXAMPLE

An 8-in. (203-mm) thick, 20 ft (6.10 m) high reinforced simply supported concrete masonry wall (115 pcf (1,842 kg/m³)) is to be designed to resist wind load as well as eccentrically applied axial live and dead loads as depicted in Figure 9. The designer must determine the reinforcement size spaced at 24 in. (610 mm) required to resist the applied loads, listed below.

D = 520 lb/ft (7.6 kN/m), at e = 0.75 in. (19 mm)
L = 250 lb/ft (3.6 kN/m), at e = 0.75 in. (19 mm)
W = 20 psf (1.0 kPa)

The maximum moment due to the wind load is determined as follows.

The axial load used for design is the axial load at the location of maximum moment. This combination may not necessarily be the most critical section for combined axial load and flexure, but should be close to the critical location. The wall weight is estimated to be halfway between fully grouted and hollow (82 and 38.7 psf (400 and 189 kg/m2), respectively, for 115 pcf (1842 kg/m3) unit concrete density).

The eccentricity of the axial loads also induces bending in the wall and should be included in the applied moment. The magnitude of the moment due to the eccentric axial load must be found at the same location as the maximum moment.

During design, all load combinations should be checked, with the controlling load case used for design. For brevity, only the two combinations above will be evaluated here, since the axial load actually increases the flexural capacity for the first combination by offsetting tension in the wall due to the lateral load.

Figure 2 shows that No. 4 bars at 24 in. (M #13 at 610 mm) on center are adequate. If a larger bar spacing is desired, No. 5 at 32 in. (M #16 at 813 mm) or No. 6 at 48 in. (M #19 at 1219 mm) will also meet the design requirements. Although wall design is seldom governed by out-of-plane shear, the shear capacity should be checked. In addition, the axial load should be recalculated based on the actual wall weight (based on grout spacing chosen), then the resulting required capacity should be recalculated and plotted on the interaction diagram to check adequacy.

Figure 9 -Wall Section for Loadbearing Wall Design Example

NOMENCLATURE

D dead load, lb/ft (kN/m)
e eccentricity of axial load – measured from centroid of wall, in. (mm)
f’_m specified masonry compressive strength, psi (MPa)
h height of wall, in. (mm)

L live load, lb/ft (kN/m)
L_r roof live load, lb/ft (kN/m)

M_u factored moment, in.-lb/ft or ft-lb/ft (kN⋅m/m)
P_u factored axial load, lb/ft (kN/m)

s spacing of vertical reinforcement, in. (mm)
W wind load, psf (kN/m²)
y distance measured from top of wall, ft (m)

REFERENCES

Strength Design of Concrete Masonry, TEK 14-04B. Concrete Masonry & Hardscapes Association, 2002.
Loadbearing Concrete Masonry Wall Design, TEK 14-05A. Concrete Masonry & Hardscapes Association, 2006.
Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Structures Joint Committee, 2002.
Concrete Masonry Wall Design Software, CMS-10. Concrete Masonry & Hardscapes Association, 2002.
Concrete Masonry Design Tables, TR 121A. Concrete Masonry & Hardscapes Association, 2000.
Minimum Design Loads for Buildings and Other Structures, ASCE 7-02. American Society of Civil Engineers, 2002.

Allowable Stress Design of Pier and Panel Highway Sound Barrier Walls

August 2018

INTRODUCTION

Sound barrier walls are increasingly being used to reduce the impact of traffic noise on properties abutting major urban traffic routes. Because concrete masonry possesses many desirable features and properties—excellent sound resistance, low cost, design flexibility, structural capability and durability, it is an excellent material for the design and construction of highway sound barrier walls.

Aesthetics is also an important consideration. Noise barriers significantly impact a highway’s visual impression. Visual qualities of noise barriers include overall shape, end conditions, color, texture, plantings and artistic treatment.

The variety of concrete masonry surface textures, colors and patterns has led to its extensive use in sound barrier walls.

Various types of concrete masonry walls may be used for sound barriers. Pier and panel walls are relatively easy to build and are economical due to the reduced thickness of the walls and the intermittent pier foundations. In addition, the piers can be offset with respect to the panels to achieve desired aesthetic effects. Pier and panel walls are also easily adapted to varying terrain conditions and are often used in areas that have expansive soils.

This TEK presents information on the structural design of concrete masonry pier and panel sound barrier walls. Requirements and considerations for reduction of highway traffic noise are discussed in TEK 13-03A, Concrete Masonry Highway Noise Barriers (ref. 2).

DESIGN

Building Code Requirements for Masonry Structures, ACI 530/ASCE 5/TMS 402 (ref. 1) includes requirements for allowable stress design, strength design and prestressed approaches. The allowable stress design approach was used to develop the designs in this TEK. Allowable stresses were increased by one-third, as permitted for load combinations which include wind or seismic loads. Allowable Stress Design of Concrete Masonry, TEK 14-07C (ref. 4), describes the basic design approach.

Materials and Workmanship

Since concrete masonry sound barrier walls are subject to a wide range of load conditions, temperatures and moisture conditions, the selection of proper materials and proper workmanship is very important to ensure durability and satisfactory structural performance. Accordingly, it is recommended that materials (concrete masonry units, mortar, grout and reinforcement) comply with applicable requirements contained in Building Code Requirements for Masonry Structures (ref. 1).

Lateral Loads

Design lateral loads should be in accordance with those specified by local or state building and highway departments. If design lateral loads are not specified, it is recommended that they conform to those specified in Minimum Design Loads for Buildings and Other Structures, ASCE 7 (ref. 3). Wind and earthquake loads required in this standard are briefly described in the following paragraphs.

Design wind loads (F) on sound barrier walls may be determined as follows:

For the wall designs in this TEK, G is taken as 0.85 and C as 1.2. The minimum wind load specified in ASCE 7 is f 10 psf (479 Pa). For basic wind speeds of 85 mph (minimum), 90 mph, 100 mph, and 110 mph (53, 145, 161, and 177 kmph), the corresponding wind loads are listed in Table 1.

Earthquake loads (F ) on sound barrier walls may be p determined as follows, considering the wall system as a reinforced masonry non-building structure (ref. 3):

Seismic loads for a range of conditions are listed in Table 3.

Table 1—Wind Loads for Sound Barrier Walls

Table 2— Design Assumptions for Tables 4, 5, and 6

Table 2—Seismic Loads for Sound Barrier Walls

Deflections

Deflection considerations typically govern wall design for long spans and taller walls with greater lateral loads. Deflections are imposed to limit the development of vertical flexure cracks within the wall panel and horizontal flexure cracks near the base of the pier. The design information presented in this TEK is based on a maximum allowable deflection of L/240, where L is the wall span between piers.

DESIGN TABLES

Design information for pier and panel walls is presented in Tables 4 through 7. Tables 4 and 5 provide horizontal reinforcing steel requirements for 6 in. and 8 in. (152 and 203 mm) panels, respectively. Horizontal reinforcement requirements can be met using either joint reinforcement or bond beams with reinforcing bars.

Table 6 provides pier size and reinforcement requirements for various lateral loads. Table 7 lists minimum sizes for pier foundations, as well as minimum embedment depths. These components of pier and panel walls are illustrated in Figure 1.

When pier and panels are used, walls are considered as deep beams, spanning horizontally between piers. Walls support their own weight, vertically, and also must resist lateral out-of-plane wind or seismic loads. The panels are built to be independent of the piers to accommodate masonry unit shrinkage and soil movement. For this design condition, wall reinforcement is located either in the horizontal bed joints or in bond beams. Wall reinforcement is based on maximum moments (M) and shears (V) in the wall panels, determined as follows:

The wall panels themselves are analyzed as simply supported beams, spanning from pier to pier.

In addition to the horizontal reinforcement, which transfers lateral loads to the piers, vertical reinforcement in the panels is required in Seismic Design Categories (SDC) C, D, E and F. Building Code Requirements for Masonry Structures (ref. 1) includes minimum prescriptive reinforcement as follows. In SDC C, vertical No. 4 (M #13) bars are located within 8 in. (203 mm) of the wall ends, and at 10 ft (3.0 m) on center along the length of the wall; minimum horizontal reinforcement requirements are satisfied by the primary reinforcement listed in Tables 4 and 5. In SDC D, E and F, vertical No. 4 (M #13) bars are located within 8 in. (203 mm) of the wall ends, and at 4 ft (1.22 m) on center along the length of the wall.

Table 6 shows pier size and vertical reinforcement requirements. Piers are designed as vertical cantilevers, not bonded with the walls, and pier reinforcement is based on maximum moment and shear, determined as follows:

Design assumptions for the pier and panel walls are given in Table 2. Note that allowable stresses were increased by one-third, as permitted for load combinations which include wind or seismic loads (ref. 1).

Requirements for concrete foundations supporting the concrete masonry piers are given in Table 7. These foundations can be constructed economically by drilling. The concrete foundation piers should contain vertical reinforcement (same as shown in Table 6) which should be properly lapped with vertical reinforcement in the concrete masonry piers. The embedment depths given in Table 7 are based on an allowable lateral passive soil pressure of 300 psf (14.4 kPa).

Table 4—6 in. (152 mm) Panel Wall Reinforcement

Table 5—8 in. (203 mm) Panel Wall Reinforcement

Table 7—Pier Foundation Requirements, Minimum Embedment/Diameter

DESIGN EXAMPLE

A pier and panel highway sound barrier is to be designed using the following parameters:

6 in. (152 mm) panel thickness
10 ft (3.05 m) wall height
14 ft (4.27 m) wall span
open terrain, stiff soil
basic wind speed is 90 mph (145 km/h)
S_S = 0.25, SDC B

From Table 1, the design wind load is 14.1 psf (674 Pa) for a basic wind speed of 90 mph (145 km/h) and exposure C. Using Table 3, the design seismic load is determined to be 2.8 psf (0.13 kPa) for a 6 in. (152 mm) wall grouted at 48 in. (1219 mm), or less, on center, for S_S = 0.25. Since the wind load is s greater, the wall will be designed for 14.1 psf (674 Pa).

Using Table 4, minimum horizontal panel reinforcement is either W1.7 (MW 11) joint reinforcement at 8 in. (203 mm) on center, or bond beams at 48 in. (1220 mm) on center reinforced with one No. 5 (M #16) bar. At the bottom, the panel requires a beam 16 in. (406 mm), or two courses, deep reinforced with one No. 5 (M # 16) bar (last column of Table 4). Because the wall is located in SDC B, vertical reinforcement is not required to meet prescriptive seismic requirements.

The minimum pier size is 16 x 18 in. (406 x 460 mm), reinforced with four No. 4 (M #13) bars, per Table 6. The pier foundation diameter is 18 in. (457 mm), and should be embedded at least 7.5 ft (2.29 m), per Table 7.

NOTATIONS

A_f = area normal to wind direction, ft² (m²)
C_f = force coefficient (see ref. 3)
d = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
E_m = modulus of elasticity of masonry in compression, psi (MPa)
E_s = modulus of elasticity of steel, psi (MPa)
F = design wind load, psf (Pa) (see ref. 3)
F_a = acceleration-based site factor (at 0.3 second period) (see ref. 3)
F_m = allowable masonry flexural compression stress, psi (Pa)
F_p = seismic force, psf (Pa) (see ref. 3)
F_s = allowable tensile or compressive stress in reinforcement, psi (MPa)
F_v = allowable shear stress in masonry, psi (MPa)
f’_m = specified compressive strength of masonry, psi (MPa)
G = gust effect factor (see ref. 3)
H = wall height, ft (m)
I = importance factor (see ref. 3)
I_p = component importance factor (assume equal to 1.0 for sound barrier walls) (see ref. 3)
K_d = wind directionality factor (see ref. 3)
K_z = velocity pressure exposure coefficient (see ref. 3)
K_zt = hill and escarpment factor (see ref. 3)
L = wall span, ft (m)
M = maximum moment at the section under consideration, in.-lb (N-mm)
n = ratio of elastic moduli, Es/Em
P = applied lateral force, lb (N)
q_z = velocity pressure, psf (Pa) (see ref. 3)
= 0.00256K KzKztKdv²I
R = response modification coefficient (see ref. 3)
R_p = component response modification factor (equal to 3.0 for reinforced masonry non-building structures) (see ref. 3)
S_DS = design short period spectral acceleration =⅔(FaSS), where SS varies from less than 0.25 to greater than 1.25, and Fa is dependent on SS and soil conditions at the site (see ref. 3)
S_s = mapped maximum considered earthquake spectral response acceleration at short periods (see ref. 3)
V = shear force, lb (N)
v = basic wind speed, mph (km/h) (see ref. 3)
W_p = weight of wall, psf (Pa)
w = wind or seismic load, psf (Pa)

REFERENCES

Building Code Requirements for Masonry Structures, ACI 530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
Concrete Masonry Highway Noise Barriers, TEK 13-03A. Concrete Masonry & Hardscapes Association, 1999.
Minimum Design Loads for Buildings and Other Structures, ASCE 7-02. American Society of Civil Engineers, 2002.
Allowable Stress Design of Concrete Masonry, TEK 14-07C Concrete Masonry & Hardscapes Association, 2002.

Grout for Concrete Masonry

August 2018

INTRODUCTION

Masonry grout is a cementitious mixture used to fill cores or cavities in masonry construction. While usually added for structural reasons, grout can also increase: fire ratings, security, acoustical performance, termite resistance, blast resistance, thermal storage capacity and anchorage capabilities. Grout is composed of cement, aggregate, lime (optional) and sufficient water to allow ease of placement and ensure complete filling of the grout space. With approval, admixtures may be added to the grout mix. The high initial water content of typical grout mixes compensates for water absorption by the masonry during and after grout placement. The final water-to-cement ratio is significantly reduced, thus grout develops high compressive strength despite its apparent high initial water to cement ratio.

Generally, grout is used to structurally bond wall elements into a wall system. The most common example is in reinforced construction, where grout bonds the steel reinforcing bars to the masonry, allowing them to act as one system in resisting loads. Composite walls consist of two wythes of masonry with a solidly grouted collar joint with or without reinforcing steel. Grouted cores also increase the net cross sectional area of concrete masonry and permit walls to carry higher compressive, shear loads and lateral loads. Masonry cantilever retaining walls are often solidly grouted to increase the wall’s weight, and hence resistance to overturning. Grouted masonry construction is not required to be reinforced, but typically is for design economy. Reinforced masonry construction, however, requires grout to be placed around the reinforcement.

This TEK includes information about: types of grout; grout properties; grout admixtures; and self consolidating grout. Information on grout mixing and placement and on grout testing is contained in Grouting Concrete Masonry Walls, TEK 03-02A and Grout Quality Assurance, TEK 18-08B (refs. 1, 2) respectively.

SPECIFYING GROUT

Grout Type

Grout for use in concrete masonry construction should comply with ASTM C 476, Standard Specification for Grout for Masonry (ref. 3), or the governing building code which may permit grouting options other than those in set forth in ASTM C 476 . ASTM C 476 defines two types of grout: fine and coarse. Fine grout contains sand smaller than 3/8 in. (9.5 mm) as its only aggregate, while coarse grout allows pea gravel smaller than 1/2 in. (13 mm), or other acceptable aggregate, in addition to the sand.

Aggregates for grout must comply with ASTM C 404, Standard Specification for Aggregates for Masonry Grout (ref. 4), which includes requirements for grading, impurities, soundness, and methods of aggregate sampling and testing. When an aggregate does not meet the ASTM C 404 grading requirements, it may still be used provided the requirements of ASTM C 404 section 4.2 are met. These requirements prescribe minimum and maximum aggregate sizes and a minimum grout compressive strength of 2,000 psi (13.79 MPa).

Building codes and ASTM Specifications do not recognize any appreciable compressive strength difference between fine and coarse grouts. The choice of grout type therefore depends primarily on the minimum clear dimensions of the grout space, the grout pour height and construction economics. Coarse grout is typically more economical to produce. See TEK 03-02A (ref. 1) for more information on grout space requirements and grout type selection.

Grout Proportions

ASTM C 476 allows grout mixtures to be determined either by compliance with the proportions listed in Table 1 or by those established through compressive strength testing. Written acceptance of grout mix submittals is required prior to the commencement of grouting operations (ref. 7).

Using the proportions specified in Table 1 is a simple way to demonstrate compliance with ASTM C 476.

When using the specified compressive strength method in ASTM C 476, the grout must be sampled and tested in accordance with ASTM C 1019 (ref. 5) and have a minimum compressive strength of 2,000 psi (13.79 MPa) at 28 days. It must also be mixed to a slump of 8 to 11 in. (203 279 mm) as determined by ASTM C 143/143M (ref. 6). The grout proportions used to produce a grout with acceptable physical properties are then used to produce the grout for the project.

Compressive Strength

While 2,000 psi (13.79 MPa) is the minimum compressive strength required by ASTM C 476, project requirements may require higher strengths. For instance, when the unit strength method is used to determine the specified compressive strength of the masonry, f’m, Specification for Masonry Structures (ref. 7) requires the compressive strength of the grout to equal or exceed f’m but not be less than 2,000 psi (13.79 MPa). As an economic rule of thumb, unless structural criteria dictate otherwise, it is best to balance the specified grout strength with the specified concrete masonry assembly strength so that one element of the system is not considerably stronger than the other, resulting in material overstrength and design conservatism. When using the strength design provisions of the Building Code Requirements for Masonry Structures (ref. 8), a maximum specified grout compressive strength of 5,000 psi (34.47 MPa) for concrete masonry construction is applied. This limitation is based solely on the specified compressive strength of grout and does not limit the actual field-tested grout compressive strength.

Grout Slump

Grout for masonry construction is a high slump material with a flowable consistency to ease placement and facilitate consolidation. Both the Specification for Masonry Structures (ref. 7) and ASTM C476 require grout to have a slump between 8 and 11 in. (203 – 279 mm). Grout must be fluid enough to flow into the smallest grout spaces and around any obstructions, such as reinforcing bars, joint reinforcement, anchors, ties and small mortar protrusions (fins). Lower slump grouts are usually more difficult to place. Although the high slump (high initial water cement ratio of conventional grout) may concern those familiar with lower slump cementitious products such as concrete or mortar, concrete masonry units are absorptive, and the higher water content of grout is critical to insure that in-place grout has sufficient remaining water, after absorption by the masonry units, for cement hydration. Despite grout’s relatively high water to cement ratio, studies have shown that adequate grout compressive strengths and bond strengths are achieved even when using high slump grouts in wet concrete masonry units (ref. 9).

While both codes and standards specify grout slumps in excess of 8 in. (203 mm), there may be certain conditions where lower slumps could be used or may be warranted. For example, if the concrete masonry units are low absorptive units or if the grout spaces are large and the grout lifts are short, lower water content grouts may work fine although care should be taken to assure adequate filling around reinforcement or other obstructions. Likewise, cold weather could present conditions where lower water content grout would be advantageous under certain circumstances (i.e. freezing conditions), but not as a general rule. For demonstrating the suitability of alternate grouting means and/or methods, the grout demonstration panel option detailed in Specification for Masonry Structures (ref. 7) should be used to qualify the proposed method. See CMHA TEK 03-02A (ref. 1) for information on grout demonstration panels.

Production Methods

Production methods for grout are also described in ASTM C 476. These include various forms of site-mixed and ready mixed grout. When cementitious materials and aggregates are stored separately on site and then proportioned into the mixer, they are required to be mixed for at least 5 minutes in a mechanical mixer with sufficient water to bring the grout to the desired consistency. Factory dry blended cementitious materials and aggregate can also be delivered to the job site and must be mixed for the same 5 minute time period. Another option is for the individual dry ingredients to be shipped to the job site in compartments and then mixed with water on site using continuous proportioning equipment and auger mixing to the desired consistency. Grout also may arrive at the job site in a wet-mixed condition. Ready-mixed grout may have the slump adjusted at the site to bring it to the desired consistency. If water is added, the grout must be remixed for at least 1 minute before discharging. When approved by the specifier, grout may be mixed by hand instead of a mechanical mixer when only small volumes are required.

Grout quantities required on a job can vary depending on the specific circumstances of the project. The unit properties, such as absorption and configuration, can have a significant impact.

The delivery method (pumping versus bucketing) can also introduce different amounts of waste. Although the absolute volume of grout waste seen on a large project may be larger than on a comparable small project, smaller projects may experience a larger percentage of grout waste. Table 2 provides guidance for estimating grout quantities.

ADMIXTURES

A variety of admixtures is available to enhance certain grout properties. However, ASTM C 476 requires admixtures to be included in the project documents or to be approved by the purchaser. Likewise, Specification for Masonry Structures (ref. 7) requires admixtures to be accepted by the architect or engineer. Antifreeze compounds, used to lower the freezing point of grout, are prohibited by ASTM C 476. Admixtures containing chlorides should also not be used in grout, because chlorides may corrode steel reinforcement and can contribute to efflorescence in the wall. Several admixtures are available that provide a combination of desirable characteristics, such as shrinkage compensating, plasticizing and retarding. As with any admixture, manufacturer’s directions and dosage rates should be carefully followed. Note that individual admixture results can vary from one cement supplier to another.

Superplasticizers

Superplasticizing admixtures are used to reduce the water content of a plastic cementitious mix while maintaining high flow consistency. They are not normally used in conventional grout (except self consolidating grout) since the excess water is absorbed into the masonry units. In some areas, however, this absorption of excess water has resulted in efflorescence problems. Superplasticizers have been found effective in reducing this problem by reducing the amount of water available for absorption. It should be noted however, that special formulation skills are required to ensure that the grout remains fluid long enough to completely fill all the voids.

Accelerators

In grout, accelerating admixtures increase both the rate of hydration and the amount of heat generated during hydration. They are used in cold weather to decrease grout setting time and increase the rate of strength gain. The increased heat of hydration does not eliminate the need for cold weather protection requirements. Accelerators should be free of chloride materials and not perpetuate the corrosion of embedded metals.

Shrinkage Compensators

Shrinkage compensating admixtures cause a slow, controlled grout expansion that is intended to offset grout shrinkage due to the initial water loss. These admixtures may be especially useful for high-lift grouting, where a large volume of grout is placed and consolidated at one time.

Retarders

Retarding admixtures are used in hot weather to keep the grout workable long enough for placement, consolidation and reconsolidation. They may also be used when the grout cannot be placed right away, as may be the case when the plastic grout will travel a long distance to the job site.

Fly Ash and Blast-Furnace Slag

Fly ash is a by-product of coal combustion, and is not usually thought of as an admixture in the same sense as the chemical admixtures discussed above. Fly ash can be used in grout as a pumping aid or to provide a greater slump with less water. Fly ash can also replace some of the portland cement in the grout mix, which has an economic advantage since the unit cost of fly ash is less than that of portland cement.

Addition rates of fly ash and raw natural pozzolans (ref. 10) or blast furnace slag (ref. 11) are governed by ASTM C 595, Standard Specification for Blended Hydraulic Cements (ref. 12). These products can produce grout mixes with a slower initial strength gain, which may need to be considered in cold weather to achieve the minimum compressive strength previously discussed.

SELF-CONSOLIDATING GROUT

A new grout material is becoming increasingly known in North American masonry markets – self-consolidating grout (SCG). SCG is a highly fluid and stable grout mix that is easy to place and does not require consolidation or reconsolidation. SCG’s mix design is significantly different from conventional grout. SCG is similar in nature to conventional grout, with the exception that the proportions of constituent materials are highly controlled and admixtures (typically in the form of superplasticizers with or without viscosity modifiers) are used to produce a plastic grout with desired properties. Controlled aggregate gradation is also important to maintain fluidity without segregation, to produce a mix that results in consistent properties throughout the grout lift.

Because of the fluid nature of the material, traditional measures of consistency and flow such as the slump cone test (ASTM C 143) are not applicable to SCG. A slump flow test is used instead, which is an adaptation of the conventional slump cone test. In the slump flow test, SCG is loaded into an inverted slump cone. The cone is removed and the flow of the material is observed and measured. Typical slump flow spreads for SCG range from 20 to 30 in. (508-762 mm). Indications of bleeding or segregation should not be seen in the flow spread.

SCG is a relatively new material so it is not yet incorporated into building codes and standards. To date, compliance has been achieved in several cases by using the grout demonstration panel option in Specification for Masonry Structures (ref. 7). Work is under way to standardize and codify this material.

REFERENCES

Grouting Concrete Masonry Walls, TEK 03-02A, Concrete Masonry & Hardscapes Association, 2005.
Grout Quality Assurance, TEK 18-08B, Concrete Masonry & Hardscapes Association, 2005.
Standard Specification for Grout for Masonry, ASTM C 476-02. ASTM International, 2002.
Standard Specification for Aggregates for Masonry Grout, ASTM C 404-04. ASTM International, 2004.
Standard Test Method for Sampling and Testing Grout, ASTM C 1019-03. ASTM International, 2003.
Standard Test Method for Slump of Hydraulic-Cement Concrete, ASTM C 143/143M-03. ASTM International, 2003.
Specification for Masonry Structures, ACI 530.1-05/ASCE 6-05/TMS 602-05. Reported by the Masonry Standards Joint Committee, 2005.
Building Code Requirements for Masonry Structures, ACI 530-05/ASCE 5-05/TMS 402-05. Reported by the Masonry Standards Joint Committee, 2005.
The Effects of Concrete Masonry Unit Moisture Content on Grout Bond and Grout Compressive Strength, MR 11. Concrete Masonry & Hardscapes Association Research and Development Laboratory, 1997.
Standard Specification for Coal Fly Ash and Raw or Calcined Natural Pozzolan for Use in Concrete, ASTM C 618-03. ASTM International, 2003.
Standard Specification for Ground Granulated Blast Furnace Slag for Use in Concrete and Mortars, ASTM C 989-05. ASTM International, 2005.
Standard Specification for Blended Hydraulic Cements, ASTM C 595–03. ASTM International, 2003.

Self-Consolidating Grout for Concrete Masonry

August 2018

INTRODUCTION

Self-consolidating grout (SCG) is a specially-formulated grout for use with reinforced masonry. It is designed to fill the long, narrow and sometimes highly congested cores of reinforced walls without the need for consolidation and reconsolidation by mechanical vibration or by puddling.

Self-consolidating grout has been used in various parts of the United States, under the grout demonstration panel provisions of Specification for Masonry Structures (refs. 1, 2), which is included by reference in the International Building Code (refs. 3, 4). The 2008 edition of Specification for Masonry Structures (ref. 5), however, includes explicit provisions for SCG.

Unlike conventional grout and conventional concrete, self consolidating grout (SCG) is a special application of self consolidating concrete (SCC) that uses aggregates complying with ASTM C 404, Standard Specification for Aggregates for Masonry Grout (ref. 6), as specified in ASTM C 476, Standard Specification for Grout for Masonry (ref. 7).

Similar to conventional grout, there are two types of selfconsolidating grout, coarse and fine, with the latter containing only fine aggregate. Coarse self-consolidating grout has been the most common, although fine SCG is predominant in several specific regions of the U.S.

MATERIALS FOR SELF-CONSOLIDATING GROUT

Self-consolidating grout attains a high flow not from adding more water, but from a careful mix design to create a flowable yet highly cohesive grout that will not segregate and can pass freely through congested reinforcement and narrow openings without “blocking or bridging.” SCG must maintain its fluidity without segregation and maintain consistent properties throughout the grout lift. It is composed of aggregates, cementitious materials, water and special admixtures which provide the fluidity and stability to meet performance requirements.

Aggregate Size and Proportion

To obtain the desired filling and placing ability, aggregates used in SCG should meet the requirements of ASTM C 404, as specified in ASTM C 476. The requirements for coarse aggregate, for use in coarse SCG, are essentially the same as the requirements for No. 8 and No. 89 coarse aggregate in ASTM C 33, Standard Specification for Concrete Aggregates (ref. 8): they should be either a Size No. 8 or Size No. 89 gravel, stone or air-cooled iron blast furnace slag with 100% passing the ½ in. (13 mm) sieve and at least 85 to 90% passing the 3/8 in. (9.5 mm) sieve. Fine aggregate, for use in either coarse or fine SCG, is typically Size No. 1, which is a concrete sand as defined in ASTM C 33, but could also be Size No. 2, which is a sand for masonry mortar as defined in ASTM C 144, Specification for Aggregate for Masonry Mortar (ref. 9).

ASTM C 476 contains a proportion specification as well as a performance specification for masonry grout. The proportion specification specifies that coarse grout should have fine aggregate in the amount of 2 1/4 to 3 times the sum of the volume of the cementitious materials and coarse aggregate in the amount of 1 to 2 times the sum of the volume of the cementitious materials. These ASTM C 476 requirements are equivalent to s/a (sand/total aggregate) ratios of approximately 0.50 to 0.60 on an absolute volume basis. By comparison, most self-consolidating concrete mix designs have similar s/a ratios in the 0.50 to 0.60 range.

Cementitious Materials and Minus 100 (0.150 mm) Sieve Content and Composition

Grout is required to have a minimum compressive strength of 2,000 psi (14 MPa) after 28 days of curing (ref. 7). Building Code Requirements for Masonry Structures (ref. 10) sets an upper limit on the specified compressive strength of grout at 5,000 psi (34.5 MPa) at 28 days when using strength design of concrete masonry, although experience indicates that many conventional grouts develop strengths greater than this specification limit. Note that actual strengths are somewhat higher than the specified strength to assure compliance.

In the historical context of masonry materials, the term cementitious materials has commonly referred to the cement content (as well as lime in the case of masonry mortars) used in the manufacturing of masonry units, mortar or grout. In the production of SCG, however, the fraction of very fine aggregate particles present in the mix can have a significant influence on the plastic (and by association, the hardened) properties of SCG, and therefore needs to be considered in the batching of SCG. As such, the ‘powder’ content of an SCG mix, which includes both conventional cementitious materials as well as the very fine aggregate dust smaller than the 100 (0.150 mm) sieve, is monitored to ensure a stable SCG.

Adequate paste content is critical for making stable SCG mixes because the paste forms the matrix in which the particles are suspended. This paste is composed of cementitious materials (including the powder), water and entrained air, if any. The entire powder content of some mixes may contain auxiliary materials including pozzolanic and hydraulic materials, as well as ground limestone and inert fillers. These additions can improve and maintain cohesion and segregation resistance of the mix while lowering the overall cost and helping to control the ultimate strength of the mix.

Although not widely used in the U.S., ground limestone and inert fillers can be very effective in SCG mixes as a means of keeping compressive strengths to the lower range. They should be considered if they are regionally available. Fly ash can also be an effective addition because its use can help enhance the filling ability and slump flow of the mix while providing increased cohesion and reduced sensitivity to changes in water content.

Research has shown that slump flow values are increased when the fly ash replacement rates are between 20 and 40% of portland cement (ref. 11). If the goal is to control compressive strengths, Class F fly ash can be effective because it typically does not contribute as much to strength gain as Type C fly ash. GGBFS (Ground Granulated Blast Furnace Slag) has successfully been used in SCG mixes to replace some of the cement, but its high ultimate strength gain usually means that the compressive strengths of these mixes are usually similar (or sometimes higher) than straight cement mix designs. Research (ref. 12) has demonstrated that coarse SCG mixes could be made with total cementitious materials contents of 750 lb/yd3 (445 kg/m3), and possibly with 700 lb/yd3 (415 kg/m3). By comparison, a typical conventional coarse grout made to the proportion specifications of ASTM C 476 contains about 550 to 700 lb/yd3 (325 to 415 kg/m3) of cementitious materials.

Some limited testing in the CMHA research (ref. 12) demonstrated that fine SCG could be made with total cementitious materials contents in the range of 800 to 850 lb/yd3 (475 to 505 kg/m3). By comparison, a typical conventional fine grout made to the proportion specifications of ASTM C 476 will contain about 700 to 1,000 lb/yd3 (415 to 590 kg/m3) of cementitious materials.

Water Content

The term ‘natural slump’ describes the slump of the grout mix before the polycarboxylate is added. A common procedure for making self consolidating concrete is to set the initial water target to the amount needed to bring the mix to a ‘natural slump’ of 2 to 4 in. (51 to 102 mm). The polycarboxylate is then added to make the mix fluid enough to obtain the desired slump flow. This would also be an acceptable initial water target for making SCG, although CMHA research (ref. 12) indicated that some of the most successful batches of coarse and fine SCG made with the local materials used in the research had initial water targets that yielded a ‘natural slump’ of 6 to 9 in. (152 to 229 mm) before the polycarboxylate was added.

Admixtures

Admixtures are integral to the production of SCG. The primary admixture used to impart fluidity and stability to the SCG mix is a class of high-range water-reducing admixtures known as polycarboxylates (PC). These long-chain polymers are synthesized to help keep the cement grains dispersed while adding some cohesiveness and stability to the SCG mix.

Another class of admixtures often used to make SCG in conjunction with the PC is the Viscosity-Modifying Admixtures (VMA). VMAs help adjust viscosity and can improve the cohesiveness and stability of the mix while allowing it to flow without segregation. Not all PC and VMA products have the same properties. Some PCs impart substantial amounts of stability and cohesiveness to the mix and are recommended to be used without VMA, while others benefit from the addition of VMA.

In the past (before polycarboxylates), there have been indications that in some situations superplasticizers in grout for masonry structures have not performed well because they exhibited a short pot life, meaning the mix quickly lost fluidity and rapid stiffing would follow. Absorption of mix water into the surrounding masonry also negatively impacted the flow. In high-lift grouting (placing grout into grout columns as high as 24 ft (7.3 m)), enough water could be lost to cause the grout to stiffen and bridge before reaching the bottom of the grout column. With the advent of newer high-range water reducers such as polycarboxylates, however, this problem is no longer evident (ref. 13).

Note that proportioning of SCG is not permitted in the field (ref. 5). However, final adjustment of the mix, in accordance with the SCG manufacturer’s recommendations, utilizing water or the same admixture used in the mix is permitted.

SCG PLACEMENT

Self-consolidating grout is pumped or placed into spaces to be grouted using the same procedures as for conventional grout. Research has shown that with SCG there is no need to first remove mortar fins and protrusions exceeding 1/2 in. (13 mm), as is required for conventionally grouted masonry (refs. 3, 4), since SCG is fluid enough to flow around these small obstructions (ref. 13). However, it is important to note that Specification for Masonry Structures currently requires the removal of mortar fins and protrusions exceeding 1/2 in. (13 mm) for both conventional grout and SCG (ref. 5). Note that because SCG is so fluid, it will flow through gaps wider than about 3/8 in.

(10 mm). To contain the grout, therefore, it is recommended to mortar the masonry unit cross webs of cells containing grout in partially grouted construction.

In bond beams, SCG will be adequately contained using conventional grout-stop materials, such as plastic mesh. When filling intermediate bond beams using high-lift grouting, place the grout-stop material in the bed joints both above and below the bond beam to prevent the SCG from rising above the bond beam location.

Once the SCG is placed, consolidation and reconsolidation is not necessary with either coarse or fine SCG.

Documented successful lifts of 12 ft 8 in. (3.9 m) have been achieved by filling the grout columns of 8-in. (203-mm) concrete masonry walls in a single lift in less than a minute using a concrete pump (ref. 13). Other undocumented placements have placed SCG in a single 24-ft (7.3-m) lift. Twenty-four feet (7.3 mm) is the maximum pour height currently permitted by Building Code Requirements for Masonry Structures and Specification for Masonry Structures (refs. 10, 5). Note also that for SCG, grout lift height can equal the grout pour height.

Blowouts have not been shown to be a problem for conventional masonry units in this research nor in field experience. However, specialty units with reduced or removed webs, such as “H-block” or large pilaster or column units, may require reduced lift heights.

No special curing procedures are required when using SCG. When appropriate, standard hot and cold weather construction provisions should be followed, as for other masonry projects. See All-Weather Concrete Masonry Construction, TEK 03-01C (ref. 14), for more detailed information.

SCG QUALITY ASSURANCE AND QUALITY CONTROL

Specification for Masonry Structures (ref. 5) requires SCG to:

meet the material requirements of ASTM C 476,
attain the specified compressive strength or 2,000 psi (13.79 MPa), whichever is greater, at 28 days when tested in accordance with ASTM C 1019 (ref. 15),
have a slump flow of 24 to 30 in. (610 to 762 mm) as determined by ASTM C 1611 (ref. 16), and
have a Visual Stability Index (VSI) less than or equal to 1 as determined in accordance with ASTM C 1611, Appendix X.1.

The ASTM C 476 material requirements are described in Grout for Concrete Masonry, TEK 09-04A (ref. 17). Other quality assurance and quality control provisions related to SCG are described below.

Some methods commonly used for self-consolidating concrete to evaluate passing ability, like the L-Box or J-Ring, are not normally used with SCG because experience indicates that the 3/8 in. (9.5 mm) maximum aggregate size used in SCG has adequate passing ability in masonry grouting applications.

Compressive Strength Testing of SCG Mixes

The current edition of ASTM C 1019, Standard Test Method for Sampling and Testing Grout (ref. 15), addresses the testing of SCG. The procedure for testing SCG is very similar to that for conventional grout, except that SCG is placed in the mold in one lift instead of two and SCG does not need to be rodded.

Slump Flow

The slump flow test method defined in ASTM C 1611/C 1611M, Standard Test Method for Slump Flow of Self-Consolidating Concrete (ref. 16) is used to monitor the consistency of fresh, unhardened SCG and its unconfined flow potential. It is particularly useful to assess the batch-to-batch consistency of SCG supplied over time.

Because of the fluid nature of SCG, traditional measures of consistency, such as the ASTM C 143 (ref. 18) slump test, are not applicable to SCG. The slump flow test is an adaptation of the ASTM C 143 slump cone test. In the slump flow test, SCG is loaded into an inverted slump cone in a single lift without consolidation. The cone is removed and the diameter of the grout slump flow is measured (see Figure 1).

Visual Stability Index (VSI)

VSI, also defined in ASTM C 1611, is performed after the slump flow test to provide a qualitative assessment of the SCG’s stability. The SCG patty resulting from the slump flow test is examined for aggregate segregation, bleeding and evidence of a mortar halo (a cement paste or mortar ring that has clearly separated from the coarse aggregate, around the outside circumference of the SCG patty). The SCG mix is then assigned a VSI, from 0 (highly stable) to 3 (highly unstable).

Although not required by Specification for Masonry Structures, T20 (T50) records the time it takes, during the slump flow test, for the outer edge of the SCG patty to reach a diameter of 20 in. (508 mm) from the time the mold is first raised. It is an optional test for self consolidating concrete, and is similarly applicable to SCG to provide a relative measure of the unconfined flow rate and an indication of the relative viscosity of the SCG. While the actual target value for T20 (T50) can vary for different SCG mixes, it has value in verifying the consistency between SCG batches delivered to the job site.

Self-Healing Ability ‘S’ Test

The ‘S’ test can also be used to help determine the stability of an SCG mix. While this is not a standardized test method, it is adapted from a simple test that is done by some practitioners in the field. There is a common version and a modified version, which gives an indication of the relative segregation resistance of the SCG when subjected to local vibration.

The common self-healing (non-disturbed) test is performed after the slump flow, T20 (T50) and VSI have been recorded. A 10- to 12-in. (254- to 305-mm) ‘S’ is drawn in the SCG patty with a finger, making sure to scrape off the SCG all the way down to the board. The patty is observed to see if the ‘S’ will self-heal. In cases where the self healing is excellent, the SCG flows back together and there is little or no evidence of the ‘S’ remaining. In cases where the self-healing is poor, the SCG does not flow back together and the ‘S’ remains very visible with severe aggregate, paste or water segregation.

Due to observations during the CMHA research (ref. 12), a self healing (after agitate) test was created. After completing the common self-healing test, the SCG patty is vibrated and a second test, designated self-healing (after agitate), is performed. To vibrate the mix, the side of the slump flow baseplate is lightly kicked or tapped six times with a foot (three on one side followed by three on an orthogonal [right-angle] side). The ‘S’ test is then repeated and the mix is rated again.

Suitability of Segregation Tests

In the CMHA research (ref. 12); several mixes were used to determine the suitability of self-consolidating concrete segregation tests on the SCG mixes. Testing was performed to evaluate both the Column Technique for Static Segregation (ASTM C 1610) (ref. 19) and the European Sieve Segregation Test (ref. 20). It was found that these tests were not able to distinguish unstable SCG mixes from stable mixes. It is not clear if this was a function of the particular raw materials used or a general characteristic of coarse SCG mixes. The selfhealing (after agitation) test described above was found to be a much better indicator of stable and unstable mixes for SCG.

REFERENCES

Specification for Masonry Structures, ACI 530.1-02/ASCE
6-02/TMS 602-02. Reported by the Masonry Standards
Joint Committee, 2002.
Specification for Masonry Structures, ACI 530.1-05/ASCE
6-05/TMS 602-05. Reported by the Masonry Standards
Joint Committee, 2005.
International Building Code 2003. International Code
Council, 2003.
International Building Code 2006. International Code
Council, 2006.
Specification for Masonry Structures, ACI 530.1-08/ASCE
6-08/TMS 602-08. Reported by the Masonry Standards
Joint Committee, 2008.
Standard Specification for Aggregates for Masonry Grout,
ASTM C 404-07. ASTM International, Inc., 2007.
Standard Specification for Grout for Masonry, ASTM C
476-07. ASTM International, Inc., 2007.
Standard Specification for Concrete Aggregates, ASTM C
33-03. ASTM International, Inc., 2003.
Standard Specification for Aggregate for Masonry Mortar,
ASTM C 144-04. ASTM International, Inc., 2004.
Building Code Requirements for Masonry Structures, ACI
530-08/ASCE 5-08/TMS 402-08. Reported by the Masonry
Standards Joint Committee, 2008.
Studies of Self-Compacting High Performance Concrete
with High Volume Mineral Additives. Fang, W.;Jianxiong,
C.; Changhui, Y., Proceedings of the First International
RILEM Symposium on Self-Compacting Concrete, 1999,
p. 569-578.
Self-Consolidating Grout Investigation: Making and
Testing Prototype SCG Mix Designs – Report of Phase
II Research, MR31. Concrete Masonry & Hardscapes
Association, 2006.
Self-Consolidating Grout Investigation: Compressive
Strength, Shear Bond, Consolidation and Flow – Report
of Phase I Research, MR29. Concrete Masonry &
Hardscapes Association, 2006.
All-Weather Concrete Masonry Construction, TEK 03-01C,
Concrete Masonry & Hardscapes Association, 2002.
Standard Test Method for Sampling and Testing Grout,
ASTM C 1019-07. ASTM International, Inc., 2007.
Standard Test Method for Slump Flow of SelfConsolidating Concrete, ASTM C 1611/C 1611M-05.
ASTM International, Inc., 2005.
Grout for Concrete Masonry, TEK 09-04A, Concrete
Masonry & Hardscapes Association, 2005.
Standard Test Method for Slump of Hydraulic-Cement
Concrete, ASTM C 143-05a. ASTM International, Inc.,
2005.
Standard Test Method for Static Segregation of SelfConsolidating Concrete Using Column Technique, ASTM
C 1610/C 1610M-06. ASTM International, Inc., 2006.
The European Guidelines for Self-Compacting Concrete:
Specification, Production and Use. Self Compacting
Concrete European Project Group, 2005.

R-Values and U-Factors of Single Wythe Concrete Masonry Walls

August 2018

INTRODUCTION

Single wythe concrete masonry walls are often constructed of hollow units with cores filled with insulation and/or grout. This construction method allows insulation and reinforcement to be used to increase thermal and structural performance, respectively, without increasing the wall thickness.

U-factors and R-values are used to estimate heat flow under steady state conditions (neglecting the effects of thermal mass). These steady-state values can be used in conjunction with factors such as thermal mass, climate, and building orientation to estimate a building envelope’s thermal performance, typically using software.

This TEK lists thermal resistance (R) and thermal transmittance (U) values of single wythe walls. Cavity wall R-values are listed in TEK 06-01C, R-Values of Multi-Wythe Concrete Masonry Walls (ref. 1).

The R-values/U-factors listed in this TEK were determined by calculation using the code-recognized series-parallel (also called isothermal planes) calculation method (refs. 2, 3, 4). The method accounts for the thermal bridging (energy loss) that occurs through the webs of concrete masonry units. The method is fully described in TEK 06-01C. Alternate code approved means of determining R values of concrete masonry walls include two-dimensional calculations and testing (ref. 2).

CONCRETE MASONRY ENERGY PERFORMANCE

Although this TEK presents a compendium of concrete masonry assembly R-values and U-factors, it is important to note that R values/U-factors alone do not fully describe the thermal performance of a concrete masonry assembly.

Concrete masonry’s thermal performance depends on both its steady state thermal characteristics (described by R-value or U-factor) as well as its thermal mass (heat capacity) characteristics. The steady state and mass performance are influenced by the size, type, and configuration of masonry unit, type and location of insulation, finish materials, density of masonry, climate, and building orientation and exposure conditions.

Thermal mass describes the ability of materials to store energy. Because of its comparatively high density and specific heat, masonry provides very effective thermal storage. Masonry walls retain their temperature long after the heat or air-conditioning has shut off. This, in turn, effectively reduces heating and cooling loads, moderates indoor temperature swings, and shifts heating and cooling loads to off-peak hours.

Due to the significant benefits of concrete masonry’s inherent thermal mass, concrete masonry buildings can provide similar energy performance to more heavily insulated light frame buildings.

These thermal mass effects have been incorporated into energy code requirements as well as sophisticated computer models. Due to the thermal mass, energy codes and standards such as the International Energy Conservation Code (IECC) (ref. 5) and Energy Efficient Standard for Buildings Except Low-Rise Residential Buildings, ASHRAE Standard 90.1 (ref. 2), require less insulation in concrete masonry assemblies than equivalent light-frame systems. Although applicable to all climates, the greater benefits of thermal mass tend to be found in warmer climates (lower-numbered Climate Zones).

Although the thermal mass and inherent R-value/U-factor of concrete masonry may be enough to meet energy code requirements (particularly in warmer climates), concrete masonry assemblies may require additional insulation, particularly when designed under more contemporary building code requirements or to achieve above-code thermal performance. For such conditions, there are many options available for insulating concrete masonry construction.

Although in general higher R-values reduce energy flow through a building element, R-values have a diminishing impact on the overall building envelope energy use. In other words, it’s important not to automatically equate higher R-value with improved energy efficiency. As an example, consider a two story elementary school in Bowling Green, Kentucky. If this school is built using single wythe concrete masonry walls with cell insulation only and a resulting wall R-value of 7 hr.ft2.oF/Btu (1.23 m2.K/W), an estimate of the building envelope energy use for this structure is approximately 27,800 Btu/ft2 (87.7 kW.h/m2), as shown in Figure 1. If we increase the R-value of the wall to R14 by adding additional insulation while holding the other envelope variables constant, the building envelope energy use drops by only 2.5%, which is not in proportion to doubling the wall R-value. Figure 1 illustrates this trend: as wall R-value increases, it has less and less impact on the building envelope thermal performance.

In this example, a wall R-value larger than about R12 no longer has a significant impact on the envelope energy use. At this point, it makes more sense to invest in energy efficiency measures other than wall insulation.

When required, concrete masonry can provide assemblies with R values that exceed code minimums. For overall project economy, however, the industry recommends balancing needs and performance expectations with reasonable insulation levels.

ENERGY CODE COMPLIANCE

Compliance with prescriptive energy code requirements can be demonstrated by:

the concrete masonry wall by itself or the concrete masonry wall plus a prescribed R-value of added insulation, or
the overall U-factor of the wall.

The IECC prescriptive R-value table calls for “continuous insulation” on concrete masonry and other mass walls. This refers to insulation uninterrupted by furring or by the webs of concrete masonry units. Examples of continuous insulation include rigid insulation adhered to the interior of the wall with furring and drywall applied over the insulation, continuous insulation in the cavity of a masonry cavity wall, and exterior insulation and finish systems. These and other insulation options for concrete masonry assemblies are discussed in TEK 06 11A, Insulating Concrete Masonry Walls (ref. 6).

If the concrete masonry assembly will not include continuous insulation, there are several other options to comply with the IECC requirements—concrete masonry assemblies are not required to have continuous insulation in order to meet the IECC, regardless of climate zone.

Other compliance methods include: prescriptive U-factor tables, and computer programs which may require U-factors and heat capacity (a property used to indicate the amount of thermal mass) to be input for concrete masonry walls. See TEK 06-04B, Energy Code Compliance Using COMcheck, (ref. 7) for more detailed information. Another compliance method, the energy cost budget method, incorporates sophisticated modeling to estimate a building’s annual energy cost.

A more complete discussion of concrete masonry IECC compliance can be found in TEK 06-12E (for the 2012 IECC) (ref. 8).

CONCRETE MASONRY UNIT CONFIGURATIONS

Revisions in 2011 to ASTM C90¸ Standard Specification for Loadbearing Concrete Masonry Units (ref. 9) have significantly reduced the minimum amount of web material required for CMU. Values in this TEK are based on concrete masonry units with three webs, with each web being the full height of the unit, and having a minimum thickness as provided in historical versions of ASTM C90 (see Table 1).

The changes in C90, however, allow a much wider range of web configurations, with corresponding changes in R-values and U-factors (because the webs of a CMU act as thermal bridges, reducing the CMU web area increases the R-value of the corresponding concrete masonry assembly). More discussion on the impact of web configuration and thermal performance can be found in CMU-TEC 001-23, Concrete Masonry Unit Shapes, Sizes, Properties, and Specifications (ref. 10).

The Thermal Catalog of Concrete Masonry Assemblies (ref.11) lists R-values and U-factors of traditional units, as included here, as well as wall assemblies with smaller web areas, as now allowed by ASTM C90. The additional wall assemblies are based on:

CMU having two full-height 3/4 in. (19 mm) thick webs, and
a ‘hybrid’ system of CMU, intended to maximize thermal efficiency. The hybrid system uses the two-web units described above for areas requiring a grouted cell, and a one-web unit where grout confinement is not required.

Although the R-values/U-factors in Table 2 are based on typical 8-in. (203-mm) high concrete masonry units, 4-in. (102 mm) high units (commonly called “half-high” units) are also widely available, and other heights may be available in some markets. Because the wall R values vary so little with different unit heights, the values in Table 2 can be applied to units with heights other than 8 in. (203 mm).

U-FACTOR AND R-VALUE TABLES – TRADITIONAL THREE-WEB UNITS

Table 2 lists calculated U-factors and R-values of various thicknesses of concrete masonry walls, for concrete densities of 85 to 135 lb/ft3 (1,362 to 2,163 kg/m3), with various core fills. Table 3 shows the approximate percentage of grouted and ungrouted wall area for different vertical and horizontal grout spacings, which can be used to determine R-values of partially grouted walls (see following section).

In addition to the core insulations listed across the top of Table 2, polystyrene inserts are available which fit in the cores of concrete masonry units. Inserts are available in many shapes and sizes to provide a range of insulating values and accommodate various construction conditions. Specially designed concrete masonry units may incorporate reduced height webs to accommodate inserts. Such webs also reduce thermal bridging through masonry, since the reduced web area provides a smaller cross-sectional area for energy flow. To further reduce thermal bridging, some manufacturers have developed units with two webs rather than three. In addition, some inserts have building code approval to be left in the grouted cores, thus improving the thermal performance of fully or partially grouted masonry walls.

The values for insulated and grouted cores in Table 2 are based on the assumption that all masonry cores are insulated or grouted, respectively. In other words, for ungrouted walls and fully grouted, the values in Table 2 can be used directly. For partially grouted walls, refer to the following section.

R-values of various interior and exterior insulation and finish systems are listed in Table 4. (Note that the use of batt insulation is not recommended, due to its susceptibility moisture.) These R-values can be added to the wall R-values in Table 2. After adding the R-values, the wall U-factor can be found by inverting the total R-value (i.e., U = 1 /R) (see also the following example). Note that tables of precalculated R-values and U-factors, including the various insulation and finish systems, are available in Thermal Catalog of Concrete Masonry Assemblies.

Thermal properties used to compile the tables are listed in Table 5.

R-VALUES AND U-FACTORS OF PARTIALLY GROUTED CONCRETE MASONRY

For partially grouted walls, the values in Table 2 must be modified to account for the grouted cores, using an area weighted average approach. The first step is to determine how much of the wall area is grouted (see Table 3). The U-factor of the wall is calculated from the area-weighted average of the U-factors of the grouted area and ungrouted areas as follows:

For example, consider an 8 in. (203 mm) wall composed of hollow 105 lb/ft3 (1682 kg/m3) concrete masonry, and grouted at 48 in. (1,219 mm) o.c. both vertically and horizontally. The ungrouted cores contain polyurethane foamed-in-place insulation, and the wall is finished on the interior with gypsum wallboard.

REFERENCES

R-Values of Multi-Wythe Concrete Masonry Walls, TEK 06-01C, Concrete Masonry & Hardscapes Association, 2013.
Energy Standard for Buildings Except Low-Rise Residential
Buildings, ANSI/ASHRAE/IESNA 90.1-2010. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., 2010.
ASHRAE Handbook, Fundamentals. American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc., 2009.
Guide to Thermal Properties of Concrete and Masonry Systems. ACI 122R-02. American Concrete Institute, 2002.
International Energy Conservation Code. International Code Council, 2006, 2009, 2012.
Insulating Concrete Masonry Walls, TEK 06-11A, Concrete
Masonry & Hardscapes Association, 2010.
Energy Code Compliance Using COMcheck, TEK 06-04B, Concrete Masonry & Hardscapes Association, 2012.
Concrete Masonry in the 2012 Edition of the IECC, TEK 06-12E, Concrete Masonry & Hardscapes Association, 2012.
Standard Specification for Loadbearing Concrete Masonry Units, ASTM C90-11. ASTM International, 2011.
Concrete Masonry Unit Shapes, Sizes, Properties, and Specifications, CMU-TEC-001-23, Concrete Masonry & Hardscapes Association, 2023.
Thermal Catalog of Concrete Masonry Assemblies, Second Edition, CMU-MAN-004-12, Concrete Masonry & Hardscapes Association, 2012.

Details for Half-High Concrete Masonry Units

August 2018

INTRODUCTION

Concrete masonry offers numerous functional advantages, such as structural load bearing, life and property protection, durability and low maintenance. Half-high concrete masonry units offer the additional advantages of a veneer-like appearance in economical single wythe construction. As for all concrete masonry units, integrally colored half high brick-like units provide enduring strength and lasting resistance to fire and wind while maintaining a virtually maintenance-free façade. These attributes are appealing for both new construction and renovations in historic districts.

Many designers are turning to half-high masonry because of its economy. As an alternative to a traditional cavity wall, these walls offer the same finished appearance, exterior durability and low maintenance coupled with a shorter construction time because of the single wythe loadbearing design. This TEK describes the use of half high units for single wythe masonry construction. For veneer applications, see Refs. 1 and 2.

HALF-HIGH UNITS

Half-high concrete masonry units are produced to the same quality standards as other concrete masonry units. ASTM C 90 (ref. 3) governs physical requirements such as minimum compressive strength, minimum face shell and web thicknesses, finish and appearance, and dimensional tolerances.

Like other concrete masonry units, half-highs are produced in a variety of sizes, unit configurations, colors and surface textures. In addition, special shapes, such as corners and bond beam units are also available.

WALL PERFORMANCE

Structural design considerations for half-high construction are virtually the same as those for conventional concrete masonry units. One aspect that may be different for half-high units is the unit strength. Typical nonarchitectural concrete masonry units have a minimum unit strength of 1,900 psi (13.10 MPa), corresponding to a specified compressive strength of masonry, f’m, of 1,500 psi (10.34 MPa). Half high and other architectural units, however, are typically manufactured to a higher unit strength. Designers should check with producers about the strength of locally available units, with the intent of taking advantage of these higher strengths in their designs when available.

Section properties for half-high units are essentially the same as for full-height units, and the same design aids can be used for both (see Ref. 4). In addition, because the core sizes are also typically the same as for full-height units of the same thickness, considerations for maximum reinforcing bar size as a percentage of the cell area are the same as well. See Ref. 5 for more detailed information.

Because there are more horizontal mortar joints in a wall constructed using half-high units, there is slightly less concrete web area in the wall overall. Although this theoretically reduces the wall weight, in practice the wall weights of walls constructed using half-high units are within 1 psf (0.05 kPa) of those for full height units (see Ref. 6).

To facilitate the construction of bond beams, half-high bond beam units are typically available with depressed webs to accommodate horizontal reinforcement. Grouting two half-high units provides an 8 in. (203-mm) deep bond beam, as shown in Figures 1 through 3. Note that the bottom unit of the bond beam should have depressed webs to accommodate the horizontal reinforcement, but the top unit need not have depressed webs.

Performance criteria for fire resistance, energy efficiency and acoustics of half-high units can be considered to be the same as for similar full height units. See Refs. 7 through 11 for further information. In addition, detailing window openings, door openings, etc., is the same as for single wythe masonry walls constructed using full-height units.

CONSTRUCTION

Construction with half-highs is very similar to that for conventional units. Some differences include: an increased number of courses laid per wall height, greater amount of mortar needed, as well as the difference in bond beam construction noted above. Crack control considerations are the same as for full height units.

As an alternative to supporting trusses by means of a pocket in the masonry wall or by joist hangers, Figure 4 shows a unique application where half-high units have been corbelled out to provide bearing for a wood truss floor. This also provides continuous noncombustible bearing thickness without the need to stagger the joists. See Ref. 12 for additional floor and roof connection details.

As for any single wythe construction, particular care should be taken to prevent water from entering the building interior. Dry walls are attained when both the design and construction address water movement into, through and out of the wall. Considerations include potential sources of water, unit and mortar characteristics, crack control, workmanship, mortar joint tooling, flashing and weeps, sealants, and water repellents. For single wythe masonry, an integral water repellent in both the units and mortar, as well as a compatible post-applied surface water repellent are recommended. See Refs. 13 -18 for more information.

Figure 1 shows a proprietary flashing system that collects and directs water to the exterior of the wall and out weep holes, without compromising the bond at mortar joints in the face shells (see Ref. 15 for recommended flashing locations). There are a number of generic and proprietary flashing, drainage, weep, mortar dropping control, and rain screen systems available. Single wythe flashing details using conventional flashing are included in Ref. 14.

Solid grouted single wythe walls tend to be less susceptible than ungrouted or partially grouted walls to moisture penetration, since voids and cavities where moisture can collect are absent. As a result, solid grouted walls do not require flashing and weeps, although they do require other moisture control provisions, such as sealants and water repellents. For partially grouted walls, flashing should be placed in ungrouted cells.

REFERENCES

Concrete Masonry Veneers, TEK 03-06C. Concrete Masonry & Hardscapes Association, 2012.
Crack Control Strategies for Concrete Masonry Construction, CMU-TEC-009-23, Concrete Masonry & Hardscapes Association, 2023.
Standard Specification for Loadbearing Concrete Masonry Units, ASTM C 90-06b. ASTM International, Inc., 2006.
Weights and Section Properties of Concrete Masonry Assemblies, TEK 14-01B. Concrete Masonry & Hardscapes Association, 2023.
Steel Reinforcement for Concrete Masonry, TEK 12-04D. Concrete Masonry & Hardscapes Association, 2006.
Weights and Section Properties of Concrete Masonry Assemblies, TEK 14-01B, Concrete Masonry & Hardscapes Association, 2023.
Fire Resistance Ratings of Concrete Masonry Assemblies, TEK 07-01D. Concrete Masonry & Hardscapes Association, 2018.
R-Values for Single Wythe Concrete Masonry Walls, TEK 06-02C. Concrete Masonry & Hardscapes Association, 2013.
Sound Transmission Class Ratings for Concrete Masonry Walls, TEK 13-01D. Concrete Masonry & Hardscapes Association, 2012.
Noise Control With Concrete Masonry, TEK 13-02A. Concrete Masonry & Hardscapes Association, 2007.
Outside-Inside Transmission Class of Concrete Masonry Walls, TEK 13-04A. Concrete Masonry & Hardscapes Association, 2012.
Floor and Roof Connections to Concrete Masonry Walls, TEK 5-7A. Concrete Masonry & Hardscapes Association, 2001.
Water Repellents for Concrete Masonry Walls, TEK 19-01.
Concrete Masonry & Hardscapes Association, 2006.
Design for Dry Single-Wythe Concrete Masonry Walls, 19-02B. Concrete Masonry & Hardscapes Association, 2012.
Flashing Strategies for Concrete Masonry Walls, TEK 19-04A. Concrete Masonry & Hardscapes Association, 2008.
Flashing Details for Concrete Masonry Walls, TEK 19-05A.
Concrete Masonry & Hardscapes Association, 2008.
Joint Sealants for Concrete Masonry Walls, TEK 19-06A.
Concrete Masonry & Hardscapes Association, 2014.
Characteristics of Concrete Masonry Units With Integral
Water Repellents, TEK 19-07. Concrete Masonry & Hardscapes Association, 2008.
Intelligent Design, Half-High Architectural CMU. Illinois Concrete Products Association.
Building Code Requirements for Masonry Structures, ACI 530-08/ASCE 5-08/TMS 402-08. Reported by the Masonry Standards Joint Committee, 2008.

Residential Details for High Wind Areas

August 2018

INTRODUCTION

High winds subject buildings to large horizontal forces as well as to significant uplift. Reinforced concrete masonry is well suited to resist the large uplift and overturning forces due to its relatively large mass.

High wind provisions generally apply to areas where the design wind speed is over 100 mph (161 km/hr) and over three second gust as defined by ASCE 7 (ref. 10). The enclosed details represent prescriptive minimum requirements for concrete masonry buildings, based on Standard for Hurricane Resistant Residential Construction (ref. 3).

CONTINUOUS LOAD PATH

Connections between individual building elements—roof, walls, floors and foundation—are critical to maintaining structural continuity during a high wind event. The critical damage to buildings in such events typically occurs due to uplift on the roof, resulting in the loss of crucial diaphragm support at the top of the wall. A primary goal for buildings subjected to high winds is to maintain a continuous load path from the roof to the foundation. This allows wind uplift forces on the roof to be safely distributed through the walls to the foundation. If one part of the load path fails or is discontinuous, building failure may occur.

Proper detailing and installation of mechanical connectors is necessary for maintaining continuous load paths. Note that in order for connectors to provide their rated load capacity, they must be installed according to the manufacturer’s or building code specifications. In coastal areas, corrosion protection is especially important due to the corrosive environment. Note that water penetration details are not specifically highlighted in the following details. The reader is referred to references 7 through 9 for more information on preventing water penetration in concrete masonry walls. In addition to a continuously reinforced bond beam at the top of the wall around the entire perimeter of the building, vertical reinforcement must be placed throughout a wall to resist the high uplift loads and provide continuity, including: at corners and wall intersections; on each side of openings wider than 6 ft (1,829 mm); at the ends of shear segments; and where girders or girder trusses bear on the concrete masonry wall (refs. 3, 4). Each of the exterior walls on all four sides of the building and all interior walls designed as shear walls must have at least one 2 ft (610 mm) minimum section of wall identified as a shear segment to resist the high lateral loads. Longer shear segments are more effective and are recommended where possible or required by design. See Figure 1 for a summary of reinforcement requirements (ref. 3).

Reinforcement must be properly spliced to provide load path continuity. Using allowable stress design, a splice length of 40 bar diameters is required by Building Code Requirements for Masonry Structures (ref. 1) for Grade 40 reinforcement and 48 bar diameters for Grade 60 reinforcement. If the wall was designed assuming Grade 40 and Grade 60 was used for construction, however, the 40 bar diameter lap splice may still be used. See Steel Reinforcement for Concrete Masonry, TEK 12-04D (ref. 5) for standard hook requirements.

DETAILS

Exterior Loadbearing Wall

Figure 2 shows a typical loadbearing wall with a floating floor slab. Vertical reinforcement should be placed in the center of the concrete masonry cores to adequately resist both positive and negative wind pressures. Bond beam depth and minimum horizontal reinforcement varies with design wind velocity, ceiling height, roof truss span and spacing of vertical wall reinforcement. Since wind suction forces on the leeward side of a building can be essentially as high as the pressure forces on the windward side, limitations are placed on the height above grade. However, if the slab is laterally supported and tied to the concrete masonry foundation wall as shown in Figure 3, the foundation wall may be extended to 8 ft (2,440 mm) above grade (ref. 3).

Roof Truss Anchor

Figure 4 shows a typical roof truss anchor cast into the bond beam of a concrete masonry bearing wall. The required anchor load capacity depends on the design wind speed as well as the roof truss span. In addition to being rated for uplift, the anchor must be rated for horizontal forces parallel to the wall (in-plane) and perpendicular to the wall (out-of-plane).

Often, the direct embedded roof truss anchor method of connecting the roof to walls is preferred over the bolted top plate and hurricane clip method, as it generally has greater capacity and fewer connections. Additionally, the nail area available for the hurricane clip is limited by the thickness of the top plate.

Bolted Top Plate

As an alternate to the roof truss anchor, a bolted top plate may be used for the roof to wall connection (see Figure 5); however, anchor bolt spacing must be reduced (24 in. (610 mm) maximum) because the top plate is loaded in its weak direction. The detail illustrates several different connector types that are commonly used to connect the truss to the top plate.

Gable End Walls

Because of their exposure, gable end walls are more prone to damage than are hipped roofs unless the joint at the top of the end wall and the bottom of the gable (see Figure 6b) is laterally supported for both inward and outward forces. Figure 6a shows a continuous masonry gable end wall using either a raked concrete bond beam or a cut masonry bond beam along the top of full height reinforced concrete masonry gable end walls.

As an alternative, a braced gable end wall can be constructed as shown in Figure 6b by stopping the masonry of the gable end at the eave height and then using conventional wood framing to the roof diaphragm. However, unless the end wall is properly braced to provide the necessary lateral support as shown in Figure 6b, this results in a weak point at the juncture of the two materials with little capacity to resist the high lateral loads produced by high winds. The number and spacing of braces depends on design wind speed, roof slope and roof span (ref. 2, 3, 6).

Gable End Wall Overhangs

Figure 7a shows a continuously reinforced castin-place concrete rake beam along the top of the gable end wall. The beam is formed over uncut block in courses successively shortened to match the slope of the roof. A minimum of 4 in. (102 mm) is needed from the highest projected corner of block to the top of the beam. Reinforcement that is continuous with the bond beam reinforcement in the side walls is placed in the top of the beam. In this detail, an outlooker type overhang is shown where the rake beam is constructed 3½ in. (89 mm) lower than the trusses so that a pressure treated 2 x 4 (38 x 89 mm) can pass over it. A ladder type overhang detail also can be used with the concrete rake beam where the beam is constructed to the same height as the trusses similar to that shown for the cut masonry rake beam in Figure 7b.

Figure 7b shows a continuously reinforced cut masonry rake beam along the top of the gable end wall. Masonry units are cut to conform to the roof slope at the same height as the roof trusses. A 2 ¾ in. (70 mm) deep notch is cut into the tops of the concrete masonry webs to allow placement of reinforcement that is continuous with the bond beam reinforcement in the side walls. A minimum of height of 4 in. (102 mm) is needed for the cut masonry bond beam. In this figure, a ladder type overhang is shown. However, an outlooker type overhang detail can be used similar to that shown for the cast-in-place concrete rake beam in Figure 7a.

REFERENCES

Building Code Requirements for Masonry Structures, ACI
530-02/ASCE 5-02/TMS 402-02. Reported by the Masonry
Standards Joint Committee, 2002.
The Guide to Concrete Masonry Residential Construction
in High Wind Areas. Florida Concrete & Products
Association, Inc., 1997.
Standard for Hurricane Resistant Residential Construction,
SSTD 10-99. Southern Building Code Congress
International, Inc., 1999.
2000 International Building Code. International Code
Council, 2000.
Steel Reinforcement for Concrete Masonry, TEK 12-04D.
Concrete Masonry & Hardscapes Association, 2002.
Annotated Design and Construction Details for Concrete
Masonry, CMU-MAN-001-23. Concrete Masonry &
Hardscapes Association, 2003.
Design for Dry Single-Wythe Concrete Masonry
Walls, TEK 19-02B. Concrete Masonry & Hardscapes
Association, 2012.
Flashing Strategies for Concrete Masonry Walls, TEK 19-
04A. Concrete Masonry & Hardscapes Association, 2003.
Flashing Details for Concrete Masonry Walls, TEK 19-05A.
Concrete Masonry & Hardscapes Association, 2008.
Minimum Design Loads for Buildings and Other
Structures, ASCE 7-02. American Society of Civil
Engineers, 2002.

Concrete Masonry Foundation Wall Details

August 2018

INTRODUCTION

Concrete masonry is used to construct various foundation wall types, including full basement walls, crawlspace walls, stem walls and piers. Concrete masonry is well suited for below grade applications, because of its strength, durability, economy, and resistance to fire, insects and noise. The modular nature of concrete masonry allows floor plan and wall height changes to be easily accommodated as well. Concrete masonry can be used to provide a strong, durable, energy efficient and insect resistant foundation for all building types.

This TEK contains details for various types of concrete masonry foundation walls, with accompanying text as appropriate. The reader is referred to TEK 03-11, Concrete Masonry Basement Wall Construction, TEK19-03B, Preventing Water Penetration in Below Grade Concrete Masonry Walls and CMHA’s Basement Manual for more detailed design and construction information (refs. 2, 3, 4, respectively).

Footings

Footings lie under the basement, crawlspace or stem wall and transfer structural loads from the building to the supporting soil. Footings are typically cast-in-place concrete, placed beneath the frost depth to prevent damage resulting from heaving caused by freezing of water in the soil.

Footings should be placed on undisturbed native soil, unless this soil is unsuitable, weak or soft. In this case, the soil should be removed and replaced with compacted soil, gravel or concrete. Similarly, tree roots, construction debris and ice should be removed prior to placing footings.

Unless otherwise required, footings should be carefully aligned so that the concrete masonry wall will be near the center line of the footing. Although the top surface of poured concrete footings should be relatively level, it should generally not be troweled smooth, as a slightly roughened surface enhances the bond between the mortar and concrete. Concrete footing design is governed by Building Code Requirements for Structural Concrete, ACI 318 (ref. 5), and concrete foundations are constructed with tolerances conforming to the requirements of Standard Specifications for Tolerances for Concrete Construction and Materials, ACI 117 (ref. 9).

BASEMENT WALLS

Basements are typically built as conditioned space so that they can be used for storage, work or living space. Because of this, water penetration resistance is of paramount importance to basement wall design and construction.

Following recommended backfill procedures will help prevent basement wall cracking during this operation. Walls should always be properly braced to resist backfill soil loads or have the first floor diaphragm in place prior to backfilling. Otherwise, a wall designed to be supported at the top may crack or even fail from overstressing the wall. Similarly, heavy equipment, such as bulldozers or cranes, should not be operated over the backfill during construction unless the basement walls are appropriately designed for the higher resulting loads.

The top 4 to 8 in. (102 to 203 mm) of backfill should be low permeability soil so rain water absorption into the backfill is minimized. Finished grade should be sloped away from the building.

Control joints are not typically used in foundation walls due to concerns with waterproofing the joint and the fact that shrinkage is less significant in below grade walls due to relatively constant temperature and moisture conditions. If warranted, horizontal joint reinforcement can be installed as a crack control measure.

The foundation drain shown in Figures 1 and 2 can also be located on the interior side of the footing, or on both sides if necessary. The drain should be placed below the top of the footing. The optional footing drain shown, such as 2 in. (51 mm) PVC pipe at 8 ft (2400 mm) on center, allows water on the interior to reach the foundation drain. Footing drains can either be cast into the footing or constructed using plastic pipes through the bottom of the first course of masonry, directly on top of the footing.

For reinforced construction (Figure 2), reinforcing bars must be properly located to be fully functional. In most cases, vertical reinforcement is positioned towards the interior face of below grade walls to provide the greatest resistance to soil pressures.

A solid top course on the below grade concrete masonry wall spreads loads from the building above and also improves soil gas and termite resistance. Where only the top course is to be grouted, wire mesh or another equivalent grout stop material can be used to contain the grout to the top course. Note that local codes may restrict the use of foam plastic insulation below grade in areas where the hazard of termite damage is high.

STEMWALLS FOR CRAWLSPACES

Unlike basements, crawlspaces are typically designed as unconditioned spaces, either vented or unvented. Several alternate crawlspace constructions are shown in Figures 3 and 4.

Although most building codes require operable louvered vents near each corner of a crawl space to reduce moisture buildup, research has shown that the use of a moisture retardant ground cover eliminates the need for vents in many locations (ref. 6). If the crawlspace is vented, the floor, exposed pipes and ducts are typically insulated. If unvented, either the walls or the floor above can be insulated. Unvented crawlspaces must have a floor covering to minimize moisture and, where applicable, soil gas entry. A vapor retarder (typically 6-mil (0.15 mm) polyethylene, PVC or equivalent) is good practice to minimize water migration and soil gas infiltration. A 2 1/2 in. (64 mm) concrete mud slab is generally used when a more durable surface is desired for access to utilities. A thicker concrete slab may be desirable, particularly if the crawlspace will be used for storage. A dampproof coating on the exterior crawlspace wall will also help prevent water entry into the crawlspace.

STEMWALLS FOR SLAB ON GRADE

A stemwall with slab on gradesupports the wall above and often also provides a brick (ref. 7) requires a foundation pier to have a minimum nominal thickness of 8 in. (203 mm), with a nominal height not exceeding four times its nominal thickness and a nominal length not exceeding three times its nominal thickness. Note that the International Building Code, (ref. 8) allows foundation piers to have a nominal height up to ten times the nominal thickness if the pier is solidly grouted, or four times the nominal thickness if it is not solidly grouted.

REFERENCES

Annotated Design and Construction Details for Concrete Masonry, CMU-MAN-001-03, Concrete Masonry and Hardscapes Association, 2003.
Concrete Masonry Basement Wall Construction, TEK 03-11, Concrete Masonry and Hardscapes Association, 2001.
Preventing Water Penetration in Below-Grade Concrete Masonry Walls, 19-03B, Concrete Masonry and Hardscapes Association, 2012.
Basement Manual: Design and Construction using Concrete
Masonry, CMU-MAN-002-01, Concrete Masonry and Hardscapes
Association, 2001.
Building Code Requirements for Structural Concrete, ACI 318 -02.
American Concrete Institute, 2002.
2001 ASHRAE Handbook, Fundamentals. American Society
of Heating, Refrigerating and Air-Conditioning Engineers, Inc., 2001.
Building Code Requirements for Masonry Structures, ACI 530-02/
ASCE 5-02/TMS 402-02. Reported by the Masonry Standards Joint Committee, 2002.
International Building Code. International Code Council, 2000.
Standard Specifications for Tolerances for Concrete Construction and Materials, ACI 117-90. American Concrete Institute, 1990.