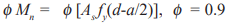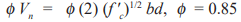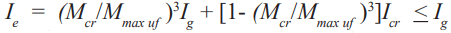Resources

INTRODUCTION

Lintels function as beams to support the wall weight and other loads over an opening, and to transfer these loads to the adjacent masonry. Because of their rigidity, strength, durability, fire resistance and aesthetics, the most common types of lintels for concrete masonry construction are those manufactured of precast reinforced concrete or reinforced concrete masonry units (ref. 3). The color and surface texture of these lintels can be used as an accent or to duplicate the surrounding masonry.

LINTEL DIMENSIONS

Precast lintel dimensions are illustrated in Figure 1. Precast concrete lintels are manufactured to modular sizes, having specified dimensions corresponding to the concrete masonry units being used in the construction.

A modular lintel length should be specified, with a minimum length of the clear span plus 8 in. (203 mm), to provide at least 4 in. (102 mm) bearing at each end (ref. 1). Additionally, if lintels are subjected to tensile stresses during storage, transportation, handling, or placement, it is recommended that steel reinforcement be provided in both the top and bottom to prevent cracking. Minimum concrete cover over the steel should be 1 ½ in. (13 mm). The lintel width, or width of the combination of side-by-side lintels, should equal the width of the supported masonry wythe.

Lintels should be clearly marked on the top whenever possible to prevent the possibility of improper installation in the wall. In the event the top of the lintel is not marked and may be installed upside down, the same size bars should be used in both the top and bottom.

LINTEL DESIGN

Precast concrete lintels are designed using the strength design provisions of Building Code Requirements for Structural Concrete, ACI 318-99 (ref. 2). In strength design, service loads are increased to account for variations in anticipated loads, becoming factored loads. The lintel is then sized to provide sufficient design strength. Further information on determining design loads for lintels is included in ASD of CM Lintels Based on 2012 IBC/2011 MSJC, TEK 17-01D (ref. 3).

Nominal lintel strength is determined based on the strength design provisions of ACI 318 and then reduced by strength reduction factors, called phi (Φ) factors. These factors account for any variability in materials and construction practices. The resulting capacity needs to equal or exceed the factored loads. Precast concrete strength reduction factors are 0.9 and 0.85 for flexure and shear, respectively (ref. 2).

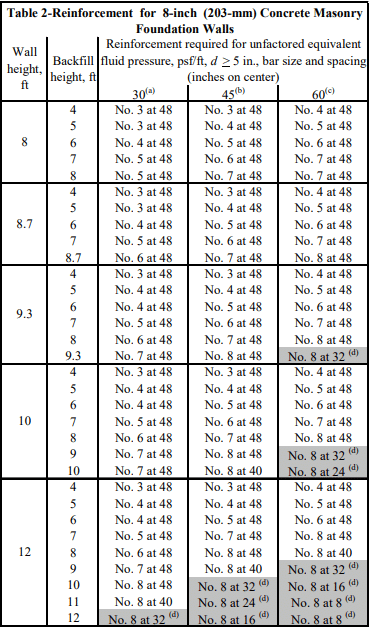
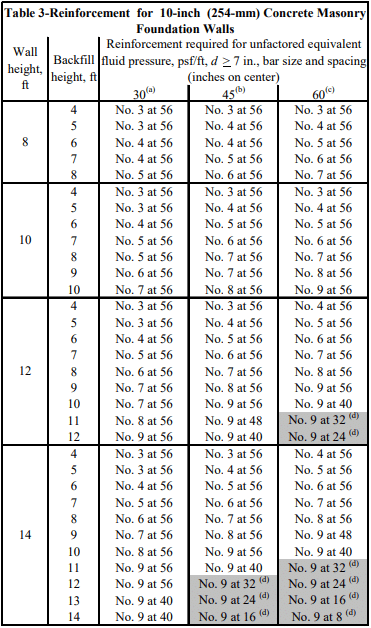
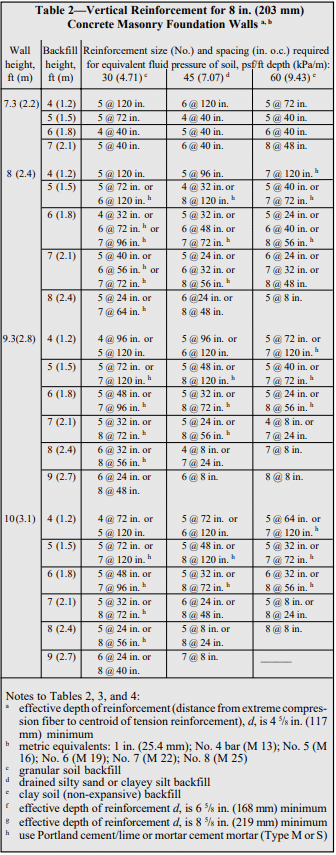
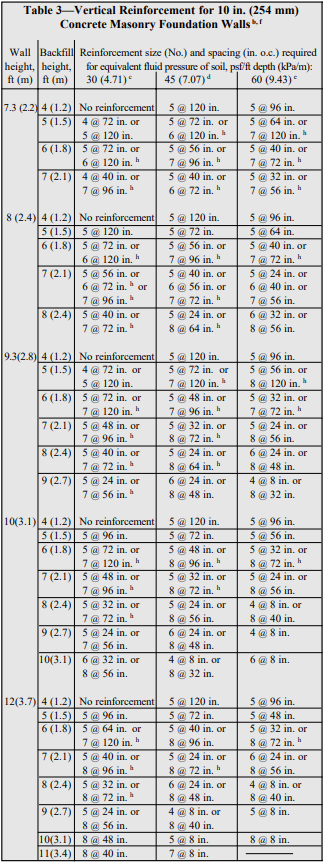
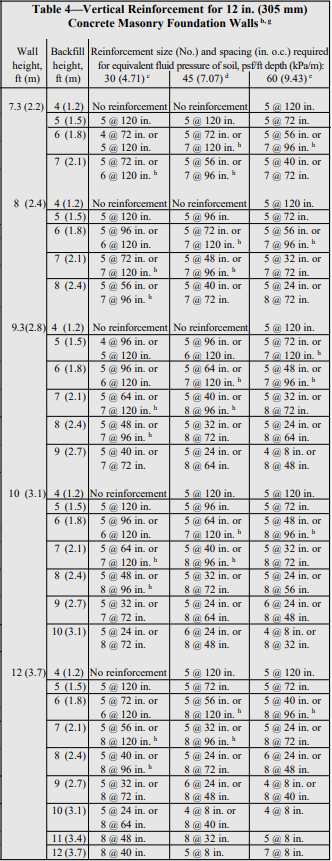
Tables 1 through 4 list design moment and shear strengths for various precast lintel sizes and concrete strengths, based on the following criteria (ref. 2).

Flexural strength:

Shear strength, no shear reinforcement:

ACI 318 contains requirements for minimum and maximum reinforcing steel areas to ensure a minimum level of performance. Minimum reinforcement area for lintels is A_{s min} = 3(f’_c)^½bd/f_y but not less than 200bd/f_y. In addition, the reinforcement ratio is limited to 75% of the balanced reinforcement ratio, ρ_max = 0.75ρ_b.

Deflection criteria for lintels is based on controlling cracking in the masonry being supported. Consequently, less deflection is allowed when the lintel supports unreinforced masonry. In this case, lintel deflection is limited to the effective span of the lintel (measured in inches) divided by 600 (L/600) (ref. 1). In addition, ACI 318 limits precast lintel deflection to L/240 when the element supported by the lintel is not likely to be damaged by large deflections, and L/480 when the element supported by the lintel is likely to be damaged by large deflections. Lintel deflection is calculated based on the effective moment of inertia, I_e, as follows (ref. 2, Section 9.5.2.3).

Shrinkage and creep due to sustained loads cause additional long-term deflections over and above those occurring when loads are first applied. ACI 318 requires that deflections due to shrinkage and creep are included, and provides an expression to estimate this additional deflection (ACI 318 Section 9.5.2.5):

λ = ξ/(1+50ρ’)

where ξ = 2.0 for exposures of 5 years or more.

DESIGN EXAMPLE

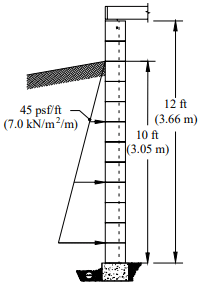
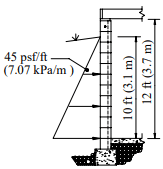
The residential basement wall shown in Figure 3 needs a lintel over the window opening. The floor live load is 400 lb (1.8 kN) per joist and the floor dead load is 100 lb (0.44 kN) per joist. Consider the floor joist loads, spaced at 16 in. (406 mm) on center, as uniformly distributed. Use a lintel self-weight of 61 lb/ ft (0.89 kN/m) and weight of 77.9 lb/ft2 (3.73 kPa) for the bond beam at the top of the wall over the lintel.

Determine effective depth, d: Assuming an 8 in. (203 mm) high lintel with two No. 4 (13M) bars,
d = 7.625 in. – 1.5 in. – 0.5/2 in.
= 5.88 in. (149 mm)

Check for arching action: The effective span length, L = 96 + 5.88 = 101.9 in. (2588 mm). Since the height of masonry above the opening is less than L/2, arching of the masonry over the opening cannot be assumed (see ref. 4 for detailed information about determining arching action).

Determine design loads:
LL = (400 lb)(12/16 in.) = 300 lb/ft (4.4 kN/m)
Dead loads include floor, wall, and lintel self-weight.
D_floor = 100 lb (12/16 in.) = 75 lb/ft (1.1 kN/m)
D_lintel = 61 lb/ft (0.89 kN/m)
D_{b beam} = (77.9lb/ft²)(7.625/12 ft)= 50 lb/ft (0.31 kN/m)
D_total = (75 + 61 + 50) = 186 lb/ft (3.2 kN/m)

For deflection calculations use loads as given above. For strength design multiply live loads by 1.7 and dead loads by 1.4. Maximum moment and shear for strength design:

M_max = wL²/8
= {[(1.7)(300)+(1.4)( 186 ) lb/ft](101.9 in.)²/8}(ft/12 in.)
= 83,328 in.-lb (9.4 kN m)

V_max = wL/2 (at distance “d” from support) (ref.2)
= [(1.7)(300)+(1.4)(186 lb/ft)](101.9/2-5.88 in.)(ft/12 in.)
= 2,893 lb (12.9 kN)

From Table 3, an 8 x 8 in. (203 x 203 mm) lintel with two No. 4 (13M) bars and f ‘_c = 4000 psi (20.7 MPa) has sufficient strength.

Check deflection: Deflection is determined using the effective moment of inertia of the lintel, I_e, calculated as follows (ref. 2).

E_c = w_c^1.533(f’_c)^½ = (150 pcf)^1.533(4000 psi)^½
= 3,834,000 psi (26,400 MPa)
f_r = 7.5(f’_c)^½ = 474 psi (3.3 MPa)
y_t = 7.625 in./2 = 3.81 in. (97 mm)
I_g = bh³/12 = (7.625 in.)(7.625 in.)³/12
= 282 in.⁴ (11,725 cm⁴)
M_cr = f_rI_g/y_t = 474 psi(282 psi)/3.81 in.
= 35,083 in.-lb (4.0 kN⋅m)
M_{max uf} = wL²/8 = [(300+186 lb/ft)(101.9 in.)²/8](ft/12 in.)
= 52567 in.-lb (5.9 kN⋅m)
(M_cr/M_{max uf})³ = (35,083/52567)³ = 0.297
n = E_s/E_c = 29,000,000/3,834,000 = 7.6
ρ = A_s/bd = 0.40 in.²/(7.625 in.)(5.88 in.) = 0.00892
nρ = 7.6(0.00892) = 0.0678
c = nρd[(1 + 2/nρ)^½ – 1]
= 0.0678(5.88 in.)[(1+ 2/0.0678)^½-1] = 1.80 in. (45 mm)
I_cr = bc³/3 + nA_s (d – c)²
= 7.625 in.(1.8 in.)³/3 + 7.6(0.4 in.²)(5.88 – 1.8)²
= 65.4 in.⁴ (2714 cm⁴)
I_e = (M_cr/M_{max uf})³ I_g + [1- (M_cr/M_{max uf})³]I_cr
= 0.297(282) + [1-0.297]65.4 in.⁴
= 130 in.⁴ (5411 cm⁴) < I_g OK

For a simply supported beam under uniform load,

∆_max = 5wL⁴/384E_cI_e
= 5(300 + 186 lb/ft)(101.9 in.)⁴/[384(3,834,000 psi)(130 in.⁴)]/(12 in./ft)
= 0.114 in. (2.9 mm)

Long-term deflection multiplier,
λ = ξ/(1+50ρ’) = 2/[1 + 50(0)] = 2

Long-term deflection,
∆_LT = λ∆_max = 2(0.114 in.) = 0.228 in. (5.8 mm)

Total deflection,
∆_tot = ∆_max + ∆_LT = 0.114 + 0.228 = 0.342 in. (8.7 mm)

Deflection limit for this case is L/240 = 101.9 in./240
= 0.42 in. (10.7 mm) > 0.342 in. (8.7 mm) OK

NOTATIONS

a             = depth of equivalent rectangular stress block, in. (mm)
A_s           = area of tension reinforcement, in.² (mm²)
b             = actual width of lintel, in. (mm)
c              = distance from extreme compression fiber to neutral axis, in. (mm)
C             = resultant compressive force in concrete, lb (kN)
d              = distance from extreme compression fiber to centroid of tension reinforcement, in. (mm)
D_{b beam}   = dead load of bond beam, lb/ft (kN/m)
D_floor      = dead load of floor, lb/ft (kN/m)
D_lintel      = dead load of lintel, lb/ft (kN/m)
D_tot         = total design dead load, lb/ft (kN/m)
E_c            = modulus of elasticity of concrete, psi (MPa)
f ‘_c           = specified compressive strength of concrete, psi (MPa)
f_r             = modulus of rupture of concrete, psi (MPa)
f_y             = specified yield strength of reinforcement, psi (MPa) (60,000 psi, 413 MPa)
I_cr            = moment of inertia of cracked section transformed to concrete, in.⁴ (cm⁴)
I_e              = effective moment of inertia, in.⁴ (cm⁴)
I_g              = moment of inertia of gross concrete section about centroidal axis, in.⁴ (cm⁴)
L               = effective length, clear span plus depth of member, not to exceed the distance between center of supports, in. (mm)
LL             = live load, lb/ft (kN/m)
M_cr           = cracking moment, in.-lb (kN⋅m)
M_max        = maximum factored moment on section, in.-lb (kN⋅m)
M_{max uf}     = maximum unfactored moment on section, in.-lb (kN⋅m)
M_n             = nominal moment strength, in.-lb/ft (kN⋅m/m)
n                = modular ratio, E_s/E_c
T                = resultant tensile force in steel reinforcement, lb (kN)
V_max          = maximum factored shear on section, lb (kN)
V_n               = nominal shear strength, lb (kN)
w                = uniform load, lb/in. (kN/m)
w_c               = density of concrete, pcf (kN/m³)
y_t                = distance from centroidal axis of gross section to extreme fiber in tension, in. (mm)
∆_max          = maximum immediate deflection, in. (mm)
∆_LT            = long-term deflection, in. (mm)
∆_tot            = total deflection, in. (mm)
ε_c               = strain in concrete, in./in. (mm/mm)
ε_s               = strain in steel reinforcement, in./in. (mm/mm)
ξ                 = time-dependent factor for sustained load
λ                 = multiplier for additional long-term deflection
Φ                = strength reduction factor
ρ                 = reinforcement ratio, A_s/bd
ρ’                = reinforcement ratio for nonprestressed compression reinforcement, A_s‘/bd
ρ_b               = reinforcement ratio producing balanced strain conditions
ρ_max           = limit on reinforcement ratio

REFERENCES

1. Building Code Requirements for Masonry Structures, ACI 530-99/ASCE 5-99/TMS 402-99. Reported by the Masonry Standards Joint Committee, 1999.
2. Building Code Requirements for Structural Concrete, ACI 318-99. American Concrete Institute, 1999.
3. ASD of CM Lintels Based on 2012 IBC/2011 MSJC, TEK 17-01D, Concrete Masonry & Hardscapes Association, 2011.